
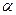 内作菱形ABCD,边长为1,∠BAD=60°,再在
内作菱形ABCD,边长为1,∠BAD=60°,再在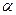 的上方,分别以△
的上方,分别以△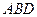 与△
与△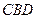 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.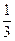 (3)
(3)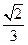
 ,垂足为M,作QN⊥平面
,垂足为M,作QN⊥平面 ,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形. ……可得ME=NE=
,垂足为N,则PM∥QN,M、N分别是正△ABD与正△BCD的中心,从而点A、M、E、N、C共线,PM与QN确定平面PACQ,且PMNQ为矩形. ……可得ME=NE=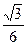 ,PE=QE=
,PE=QE=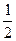 ,PQ=MN=
,PQ=MN=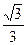 …7分∴cos∠PEQ=
…7分∴cos∠PEQ= ………9分
………9分 ∴
∴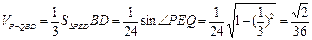 .
.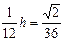 . ∴
. ∴ 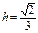 . …………………………14分
. …………………………14分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
,
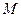 是线段
是线段 的中点.
的中点.
 ;(2)求二面角
;(2)求二面角 的大小;
的大小;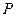 为一动点,若点
为一动点,若点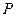 从
从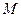 出发,沿棱按照
出发,沿棱按照
 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥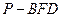 的体积的最小值.
的体积的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
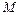 是
是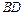 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角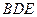 ?若存在,确定点N的位置;
?若存在,确定点N的位置;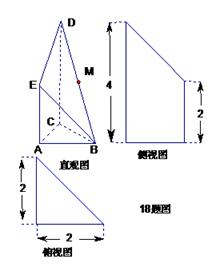
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
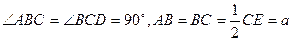 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在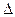 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以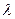 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0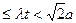 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
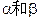 为平面,
为平面,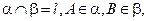 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角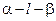 的大小为
的大小为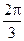 ,求:
,求: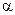 的距离;
的距离;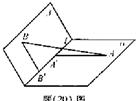
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com