
设f(n)=1+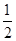 +
+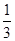 + +
+ +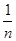 (n∈N*).
(n∈N*).
求证:f(1)+f(2)+ +f(n-1)=n·[f(n)-1](n≥2,n∈N*).
应用数学归纳法.
【解析】
试题分析:①当n=2时,左边=f(1)=1,
右边=2[1+ -1]=1,
-1]=1,
左边=右边,等式成立.
②假设n=k时,结论成立,即
f(1)+f(2)+ +f(k-1)=k[f(k)-1],
那么,当n=k+1时,
f(1)+f(2)+ +f(k-1)+f(k)
=k[f(k)-1]+f(k)
=(k+1)f(k)-k
=(k+1)[f(k+1)-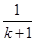 ]-k
]-k
=(k+1)f(k+1)-(k+1)=(k+1)[f(k+1)-1],
所以当n=k+1时结论仍然成立.
所以f(1)+f(2)+ +f(n-1)=n[f(n)-1](n≥2,n∈N*).
考点:本题主要考查数学归纳法。
点评:中档题,利用数学归纳法,注意遵循“两步一结”。对数学式子变形能力要求较高。


科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修2-2) 2009-2010学年 第29期 总第185期 北师大课标 题型:013
设f(n)=1+![]() +
+![]() +…+
+…+![]() (n∈N+),那么f(n+1)-f(n)=
(n∈N+),那么f(n+1)-f(n)=
![]()
![]() +
+![]()
![]() +
+![]()
![]() +
+![]() +
+![]()
查看答案和解析>>
科目:高中数学 来源:大英中学2008届高三年级第一次月考数学(理)试卷及答案 题型:044
数列{an}的通项公式![]() ,设f(n)=(1-a1)(1-a2)(1-a3)…(1-an)
,设f(n)=(1-a1)(1-a2)(1-a3)…(1-an)
(1)求f(1),f(2),f(3),f(4);
(2)猜想f(n)的计算公式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源:江西省上饶市第五中学2010-2011学年高一下期中考试数学试题A卷 题型:022
设f(n)=1+![]() +
+![]() +…+
+…+![]() (n∈N+),是否存在g(n),使得等式f(1)+f(2)+f(3)+…+f(n)+n=g(n)f(n)总成立?若存在,请写出g(n)的通项公式(不必说明理由);若不存在,请说明理由._________.
(n∈N+),是否存在g(n),使得等式f(1)+f(2)+f(3)+…+f(n)+n=g(n)f(n)总成立?若存在,请写出g(n)的通项公式(不必说明理由);若不存在,请说明理由._________.
查看答案和解析>>
科目:高中数学 来源:设计选修数学-4-5人教A版 人教A版 题型:013
(经典回放)设f(n)=1+![]() +
+![]() +…+
+…+![]() (n∈N+),则f(n+1)-f(n)等于
(n∈N+),则f(n+1)-f(n)等于
![]()
![]()
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com