
【题目】已知f(x)=x2﹣ax,g(x)=lnx,h(x)=f(x)+g(x)
(1)若f(x)≥g(x)对于公共定义域内的任意x恒成立,求实数a的取值范围;
(2)设h(x)有两个极值点x1 , x2 , 且x1∈(0, ![]() ),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
),若h(x1)﹣h(x2)>m恒成立,求实数m的最大值.
【答案】
(1)解:)f(x)≥g(x)对于公共定义域内的任意x恒成立x2﹣ax﹣lnx≥0恒成立,x>0a≤ ![]() ,x>0.
,x>0.
令u(x)= ![]() ,x>0,则u′(x)=1﹣
,x>0,则u′(x)=1﹣ ![]() =
= ![]() ,
,
当x=1时,x2+lnx﹣1=0;当x>1时,u′(x)>0,此时函数u(x)单调递增;当0<x<1时,u′(x)<0,此时函数u(x)单调递减.
因此当x=1时,函数u(x)取得极小值即最小值,u(1)=1.
∴实数a的取值范围是(﹣∞,1]
(2)解:由题意知道:h(x)=x2﹣ax+lnx.则 ![]() =
= ![]() (x>0),
(x>0),
所以方程2x2﹣ax+1=0,(x>0)有两个不相等的实数根x1,x2,且 ![]() ,
,
又∵ ![]() ,∴
,∴ ![]() ∈(1,+∞),且
∈(1,+∞),且 ![]() ,(i=1,2),
,(i=1,2),
而h(x1)﹣h(x2)= ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]()
= ![]() +
+ ![]() =
= ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() ,(x2>1)
,(x2>1)
设u(x)= ![]() (x>1),则u′(x)=
(x>1),则u′(x)= ![]() ≥0,
≥0,
∴u(x)>u(1)= ![]() ,即h(x1)﹣h(x2)>
,即h(x1)﹣h(x2)> ![]() 恒成立,
恒成立,
因此 .
∴实数m的最大值为 ![]() ﹣ln2
﹣ln2
【解析】(1)f(x)≥g(x)对于公共定义域内的任意x恒成立x2﹣ax﹣lnx≥0恒成立,x>0a≤ ![]() ,x>0.令u(x)=
,x>0.令u(x)= ![]() ,利用导数研究其单调性极值与最值即可得出.(2)由题意知道:h(x)=x2﹣ax+lnx.则
,利用导数研究其单调性极值与最值即可得出.(2)由题意知道:h(x)=x2﹣ax+lnx.则 ![]() =
= ![]() (x>0),所以方程2x2﹣ax+1=0,(x>0)有两个不相等的实数根x1 , x2 , 且
(x>0),所以方程2x2﹣ax+1=0,(x>0)有两个不相等的实数根x1 , x2 , 且 ![]() ,可得
,可得 ![]() ∈(1,+∞),且
∈(1,+∞),且 ![]() ,(i=1,2),而h(x1)﹣h(x2)=
,(i=1,2),而h(x1)﹣h(x2)= ![]() ,(x2>1)设u(x)=
,(x2>1)设u(x)= ![]() (x>1),利用导数研究其单调性极值与最值即可得出.
(x>1),利用导数研究其单调性极值与最值即可得出.


科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域R上的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.
,且g(x)=a2x+a﹣2x﹣4f(x),求g(x)在[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若an=log(n+1)(n+2)(n∈N),我们把使乘积a1a2…an为整数的数n叫做“劣数”,则在区间(1,2004)内所有劣数的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD. (Ⅰ)证明:BM⊥平面SMC;
(Ⅱ)若SB与平面ABCD所成角为 ![]() ,N为棱SC上的动点,当二面角S﹣BM﹣N为
,N为棱SC上的动点,当二面角S﹣BM﹣N为 ![]() 时,求
时,求 ![]() 的值.
的值.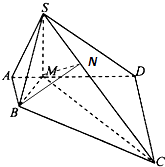
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.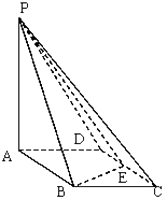
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,福建省大力推进海峡西岸经济区建设,福州作为省会城市,在发展过程中,交通状况一直倍受有关部门的关注,据有关统计数据显示上午6点到10点,车辆通过福州市区二环路某一路段的用时y(分钟)与车辆进入该路段的时刻t之间关系可近似地用如下函数给出:y= 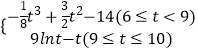 .求上午6点到10点,通过该路段用时最多的时刻.
.求上午6点到10点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强高考与高中学习的关联度,考生总成绩由统一高考的语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.保持统一高考的语文、数学、外语科目不变,分值不变,不分文理科,外语科目提供两次考试机会.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物、信息技术七科目中自主选择三科.
(1)某高校某专业要求选考科目物理,考生若要报考该校该专业,则有多少种选考科目的选择;
(2)甲、乙、丙三名同学都选择了物理、化学、历史组合,各学科成绩达到二级的概率都是0.8,且三人约定如果达到二级不参加第二次考试,达不到二级参加第二次考试,如果设甲、乙、丙参加第二次考试的总次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com