
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[ ![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)若f(x)=x+ ![]() ,函数在(0,a]上的最小值为4,求a的值;
,函数在(0,a]上的最小值为4,求a的值;
(2)对于(1)中的函数在区间A上的值域是[4,5],求区间长度最大的A(注:区间长度=区间的右端点﹣区间的左断点);
(3)若(1)中函数的定义域是[2,+∞)解不等式f(a2﹣a)≥f(2a+4).
【答案】
(1)解:由题意的:函数f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,
上单调递增,
当a> ![]() 时,即a>1时函数在x=
时,即a>1时函数在x= ![]() 处取得最小值,
处取得最小值,
∴f( ![]() )=2
)=2 ![]() =4,解得a=4,
=4,解得a=4,
当a< ![]() 时,即0<a<1时,函数在x=a处取得最小值,
时,即0<a<1时,函数在x=a处取得最小值,
∴f(a)=a+1=4,解得a=3不符合题意,舍去.
综上可得 a=4
(2)解:由(1)得f(x)=x+ ![]() ,又x=2时函数取得最小值4,
,又x=2时函数取得最小值4,
令x+ ![]() =5,则x2﹣5x+4=0,解得 x=1或 x=4,
=5,则x2﹣5x+4=0,解得 x=1或 x=4,
又2∈[1,4],
∴区间长度最大的A=[1,4]
(3)解:由(1)知函数在[2,+∞)上单调递增,
∴原不等式等价于 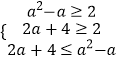 ,
,
解得a≥4或a=﹣1,
∴不等式的解集{a|a≥4或a=﹣1}
【解析】(1)利用性质,讨论 ![]() 与区间(0,a]的关系,从而利用最小值是4,建立条件关系.(2)根据值域为[4,5],确定对应的变量x,然后判断最大的区间.(3)利用函数的单调性,解不等式即可.
与区间(0,a]的关系,从而利用最小值是4,建立条件关系.(2)根据值域为[4,5],确定对应的变量x,然后判断最大的区间.(3)利用函数的单调性,解不等式即可.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷![]() 份,
份, ![]() 名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
(1)要从这![]() 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取![]() 名中小学生进一步调查,则在
名中小学生进一步调查,则在![]() (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?
(2)若希望![]() 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于![]() (小时),请估计
(小时),请估计![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=4n,数列{bn}满足b1=-3,
bn+1=bn+(2n-3)(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)若cn=![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,已知直线l1:
中,已知直线l1: ![]() (
(![]() ,
, ![]() ),抛物线C:
),抛物线C:  (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com