已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0又f(1)=-2.
(1)判断f(x)的奇偶性;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在区间[-3,3]上的值域;
(4)若?x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
(1)解:取x=y=0,则f(0+0)=2f(0),∴f(0)=0,
取y=-x,则f(x-x)=f(x)+f(-x),
∴f(-x)=-f(x)对任意x∈R恒成立,
∴f(x)为奇函数.
(2)证明:任取x
1,x
2∈(-∞,+∞)且x
1<x
2,
则x
2-x
1>0,f(x
2)+f(-x
1)=f(x
2-x
1)<0,
∴f(x
2)<-f(-x
1),
又f(x)为奇函数,∴f(x
1)>f(x
2).
故f(x)为R上的减函数;
(3)∵f(x)为R上的减函数,
∴对任意x∈[-3,3],恒有f(3)≤f(x)≤f(-3),
f(3)=3f(1)=-2×3=-6,∴f(-3)=-f(3)=-6,
故f(x)在[-3,3]上最大值为6,最小值为-6.
故f(x)在区间[-3,3]上的值域为[-6,6].
(3)解:f(x)为奇函数,整理原式得f(ax
2)+2f(-x)<f(x)+f(-2),
可得f(ax
2-2x)<f(x-2),而f(x)在R上是减函数,
所以ax
2-2x>x-2即ax
2-3x+2>0恒成立,
①当a=0时不成立,
②当a≠0时,有a>0且△<0,即
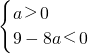
,解得a>

.
故a的取值范围为(

,+∞).
分析:(1)取x=y=0可求得f(0),取y=-x可得f(x)与f(-x)的关系,由奇偶性的定义即可判断;
(2)任取x
1,x
2∈(-∞,+∞)且x
1<x
2,由已知可得f(x
2)+f(-x
1)=f(x
2-x
1)<0,从而可比较f(x
1)与f(x
2)的大小关系,得到f(x
1)>f(x
2);
(3)由(2)知f(x)的单调性,根据单调性即可求得最大值、最小值,从而求得值域;
(4)根据函数的奇偶性、单调性可把f(ax
2)+2f(-x)<f(x)+f(-2)转化为具体不等式恒成立,利用数形结合即可得到关于a的限制条件,解出即可.
点评:本题考查抽象函数 的奇偶性、单调性及其应用,考查函数恒成立问题,考查学生分析问题解决问题的能力,属中档题.

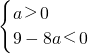 ,解得a>
,解得a> .
. ,+∞).
,+∞).
