
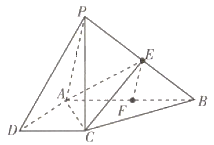
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,F是
,F是![]() 的中点,E是
的中点,E是![]() 上的一点,则下列说法正确的是( )
上的一点,则下列说法正确的是( )
A.若![]() ,则
,则![]() 平面
平面![]()
B.若![]() ,则四棱锥
,则四棱锥![]() 的体积是三棱锥
的体积是三棱锥![]() 体积的6倍
体积的6倍
C.三棱锥![]() 中有且只有三个面是直角三角形
中有且只有三个面是直角三角形
D.平面![]() 平面
平面![]()
【答案】AD
【解析】
利用中位线的性质即可判断选项A;先求得四棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 的体积的关系,再由四棱锥
的体积的关系,再由四棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的关系进而判断选项B;由线面垂直的性质及勾股定理判断选项C;先证明
的关系进而判断选项B;由线面垂直的性质及勾股定理判断选项C;先证明![]() 平面
平面![]() ,进而证明平面
,进而证明平面![]() 平面
平面![]() ,即可判断选项D.
,即可判断选项D.
对于选项A,因为![]() ,所以
,所以![]() 是
是![]() 的中点,
的中点,
因为F是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故A正确;
,故A正确;
对于选项B,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以梯形![]() 的面积为
的面积为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,故B错误;
,故B错误;
对于选项C,因为![]() 底面
底面![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() 为直角三角形,
为直角三角形,
又![]() ,所以
,所以![]() ,则
,则![]() 为直角三角形,
为直角三角形,
所以![]() ,
,![]() ,
,
则![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
故三棱锥![]() 的四个面都是直角三角形,故C错误;
的四个面都是直角三角形,故C错误;
对于选项D,因为![]() 底面
底面![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,
在直角梯形![]() 中,
中,![]() ,
,
所以![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,故D正确,
,故D正确,
故选:AD


科目:高中数学 来源: 题型:
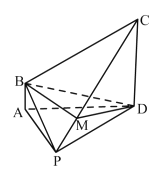
【题目】如图,在四棱锥PABCD-中,AB//CD,AB=1,CD=3,AP=2,DP=2![]() ,PAD=60°,AB⊥平面PAD,点M在棱PC上.
,PAD=60°,AB⊥平面PAD,点M在棱PC上.
(Ⅰ)求证:平面PAB⊥平面PCD;
(Ⅱ)若直线PA// 平面MBD,求此时直线BP与平面MBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的一个顶点为![]() ,焦点在x轴上,若椭圆的右焦点到直线
,焦点在x轴上,若椭圆的右焦点到直线![]() 的距离是3.
的距离是3.
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.
设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() .
.

(1)在PD上是否存在一点F,使得![]() 平面PAB,若存在,找出F的位置,若不存在,请说明理由;
平面PAB,若存在,找出F的位置,若不存在,请说明理由;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
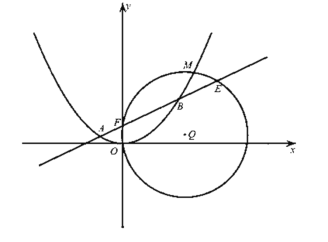
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上一点过
上一点过![]() 三点的圆的圆心为
三点的圆的圆心为![]() ,点
,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 的横坐标为4,过
的横坐标为4,过![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() ,直线
,直线![]() 与圆
与圆![]() 交于点
交于点![]() ,且点
,且点![]() 的横坐标大于4,求当
的横坐标大于4,求当![]() 取得最小值时直线
取得最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com