
(1)��˫����C��������e��ȡֵ��Χ;
(2)��ֱ��l����˫����C���ҽ���F��˫����C����P��Q����,��������![]() =
=![]()
![]() ,��˫����C�ķ���.
,��˫����C�ķ���.
(��)��֪F1��F2�ֱ�Ϊ��ԲC:![]() =1(a��b��0)�����ҽ���,ֱ��l:y=2x+5����ԲC��������P1��P2,��֪��ԲC������O����ֱ��l�ĶԳƵ�ǡ��������ԲC��������.
=1(a��b��0)�����ҽ���,ֱ��l:y=2x+5����ԲC��������P1��P2,��֪��ԲC������O����ֱ��l�ĶԳƵ�ǡ��������ԲC��������.
(1)����ԲC�����ߵķ���;
(2)���![]() a2��
a2��![]() ��
��![]() �ĵȲ�����,����ԲC�ķ���.
�ĵȲ�����,����ԲC�ķ���.
�𰸣�(��)�⣺(1)��y=x+m��������![]() =1��,��b2x2-2(x+m)2-2b2=0,������(b2-2)x2-4mx-2(m2+b2)=0,��b2=2,m=0ʱֱ����˫��������,���ֱ����˫���ߺ��й�����ì��,��b2��2.��e��
=1��,��b2x2-2(x+m)2-2b2=0,������(b2-2)x2-4mx-2(m2+b2)=0,��b2=2,m=0ʱֱ����˫��������,���ֱ����˫���ߺ��й�����ì��,��b2��2.��e��![]() .
.
��b2��2ʱ,ֱ����˫���ߺ��й�����?��=16m2+8(b2-2)(m2+b2)��0�����,��b4+b2(m2-2)��0�����,
��b2��0,��b2+(m2-2)��0.��b2��2-m2.��e2=![]() =
=![]() ��
��![]() ,m��R,
,m��R,
��(![]() )���=2.��e2��2,��e��
)���=2.��e2��2,��e��![]() .��������,e��(
.��������,e��(![]() ,+��).
,+��).
(2)��F(c,0),��ֱ��l:y=x-c,��x=y+c����˫���߷�����,��b2(y+c)2-2y2-2b2=0,
������(b2-2)y2+2cb2y+b2c2-2b2=0,��������ΪP(x1,y1),Q(x2,y2),
��y1+y2=![]() ,y1y2=
,y1y2=![]() ,��
,��![]() ,��y2=5y1.
,��y2=5y1.
��6y1=![]() ,5y12=
,5y12=![]() .��ȥy1,��
.��ȥy1,��![]() .
.
��b2��0��c2-2=b2,��![]() =
=![]() .��b2=7.������˫����C�ķ���Ϊ
.��b2=7.������˫����C�ķ���Ϊ![]() =1.
=1.
(��)�⣺(1)��O����l�ĶԳƵ�Ϊ(x0,y0),
�� ��֮,��x0=-4.
��֮,��x0=-4.
����ԲC�����ߵķ���Ϊx=-4.
(2)��P1(x1,y1),P2(x2,y2),F1(-c,0),F2(c,0),��![]() =(x1+c,y1),
=(x1+c,y1),![]() =(x2-c,y2),
=(x2-c,y2),![]() =(c,0).
=(c,0).
��![]() =c(x1+c),
=c(x1+c),![]() =c(x2-c).������,
=c(x2-c).������,![]() a2=c(x1+c)+c(x2-c)=c(x1+x2),
a2=c(x1+c)+c(x2-c)=c(x1+x2),
��x1+x2=![]() ��
��![]() .��
.��![]() =4,��x1+x2=
=4,��x1+x2=![]() .
.
��a2=4c.��b2=4c-c2.����ԲC�ķ��̿��Ի�Ϊ![]() =1.
=1.
��
![]() (20-c)x2+80x+100-16c+4c2=0.
(20-c)x2+80x+100-16c+4c2=0.
��x1+x2=![]() .��
.��![]() =
=![]() .��֮,��c=2.��a2=8,b2=4.
.��֮,��c=2.��a2=8,b2=4.
��������ԲC�ķ���Ϊ![]() =1.
=1.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| 2 |
| y2 |
| b2 |
| FP |
| 1 |
| 5 |
| FQ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
A.(1,+��) B.(![]() ,+��) C.(
,+��) C.(![]() ,+��) D.(2,+��)
,+��) D.(2,+��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
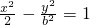 ��b��0�����й�����
��b��0�����й�����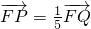 ����˫����C�ķ��̣�
����˫����C�ķ��̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�������ʡ���������и߿���ѧ��ģ�Ծ����Ŀƣ��������棩 ���ͣ������
 ��b��0���������
��b��0�����й����� ����˫����C�ķ��̣�
����˫����C�ķ��̣��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com