
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
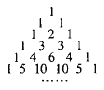
A. 110B. 114C. 124D. 125
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数m的取值范围是( )
若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数m的取值范围是( )
A.[1,4)B.(1,4)C.(![]() )D.[
)D.[![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于M.N点.
的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于M.N点.
(1)若![]() ,
,![]() 的面积为
的面积为![]() ,求抛物线方程;
,求抛物线方程;
(2)若A.M.F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到直线n、m距离的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,
(x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,![]() ).
).
(Ⅰ)若f(x)≥0在x∈R上恒成立,求实数a的取值范围;
(Ⅱ)若ex≥lnx+m对任意x>0恒成立,求证:实数m的最大值大于2.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市疾控中心流感监测结果显示,自![]() 年
年![]() 月起,该市流感活动一度出现上升趋势,尤其是
月起,该市流感活动一度出现上升趋势,尤其是![]() 月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知
月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知![]() 位同学中有
位同学中有![]() 位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
方案乙:先任取![]() 个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这
个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这![]() 位中的
位中的![]() 位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外
位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外![]() 位同学中逐个检测;
位同学中逐个检测;
(1)求依方案甲所需化验次数等于方案乙所需化验次数的概率;
(2)![]() 表示依方案甲所需化验次数,
表示依方案甲所需化验次数,![]() 表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com