
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)经过点(﹣1,
=1(a>b>0)经过点(﹣1, ![]() ),其离心率e=
),其离心率e= ![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l:y=kx+m与椭圆C相切,切点为T,且l与直线x=﹣4相交于点S.
试问:在x轴上是否存在一定点,使得以ST为直径的圆恒过该定点?若存在,求出该点的坐标;若不存在,请说明理由.
【答案】解:(Ⅰ)由点(1, ![]() )在椭圆上得,代入椭圆方程:
)在椭圆上得,代入椭圆方程: ![]() ,①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
,①﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
椭圆的离心率e= ![]() =
= ![]() ,则a=2c,a2=4c2 , b2=3c2 , ②
,则a=2c,a2=4c2 , b2=3c2 , ②
②代入①解得c2=1,a2=4,b2=3,
故椭圆C的标准方程为 ![]() ;
;
(Ⅱ)由 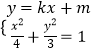 ,消去y,整理得(4k2+3)x2+8kmx+4m2﹣12=0;
,消去y,整理得(4k2+3)x2+8kmx+4m2﹣12=0;
因为动直线l与椭圆C相切,即它们有且只有一个公共点T,可设T(x0 , y0),
m≠0,△=0,∴(8km)2﹣4×(4k2+3)×(4m2﹣12)=0,
∴4k2﹣m2+3=0,③﹣﹣﹣﹣
此时,x0= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,y0=kx0+m=
,y0=kx0+m= ![]() ,则T(﹣
,则T(﹣ ![]() ,
, ![]() ).由
).由 ![]() ,得S(4,4k+m).假设平面内存在定点满足条件,不妨设为点A.
,得S(4,4k+m).假设平面内存在定点满足条件,不妨设为点A.
由图形对称性知,点A必在x轴上.设A(x1 , 0),则由已知条件知AS⊥AT,
即 ![]()
![]() =0对满足③式的m,k恒成立.由
=0对满足③式的m,k恒成立.由 ![]() =(4﹣x1 , 4k+m),
=(4﹣x1 , 4k+m), ![]() =(﹣
=(﹣ ![]() ﹣x1 ,
﹣x1 , ![]() ),由
),由 ![]()
![]() =0得:﹣
=0得:﹣ ![]() +
+ ![]() ﹣4x1+x12+
﹣4x1+x12+ ![]() +3=0,
+3=0,
整理得(4x1﹣4) ![]() +x12﹣4x1+3=0,④由②式对满足①式的m,k恒成立,则
+x12﹣4x1+3=0,④由②式对满足①式的m,k恒成立,则 ![]() ,解得x1=1.
,解得x1=1.
故平面内存在定点(1,0),使得以ST为直径的圆恒过该定点.
【解析】(Ⅰ)由题意可知:将点代入椭圆方程,利用椭圆的离心率公式即可求得a和b的值,即可求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,由△=0,求得4k2﹣m2+3=0,利用韦达定理及中点坐标公式,求得T点坐标,联立即可求得S点坐标,由 ![]()
![]() =0,根据向量数量积的坐标运算,可得
=0,根据向量数量积的坐标运算,可得 ![]() ,即可求得A点坐标,即可求得以ST为直径的圆恒过该定点(1,0).
,即可求得A点坐标,即可求得以ST为直径的圆恒过该定点(1,0).


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCFE中,四边形EFCB为梯形,EF∥BC,且EF= ![]() BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG=
BC,△ABC是边长为2的正三角形,顶点F在AC上的射影为点G,且FG= ![]() ,CF=
,CF= ![]() ,BF=
,BF= ![]() .
. 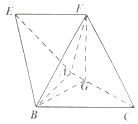
(1)证明:平面FGB⊥平面ABC;
(2)求二面角E﹣AB﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣alnx﹣(a﹣2)x.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2(1)求满足条件的最小正整数a的值;
(Ⅲ)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量![]() (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当![]() 时,为酒后驾车;当
时,为酒后驾车;当![]() 时,为醉酒驾车.某市交通管理部门于某天晚上8点至11点设点进行一次拦查行动,共依法查出60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中
时,为醉酒驾车.某市交通管理部门于某天晚上8点至11点设点进行一次拦查行动,共依法查出60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中![]() 的人数计入
的人数计入![]() 人数之内).
人数之内).

1)求此次拦查中醉酒驾车的人数;
2)从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究,再从抽取的8人中任取2人,求两人中恰有1人醉酒驾车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
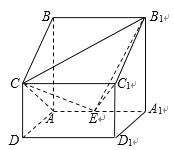
(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长度;
的长度;
(Ⅲ)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?(结论不要求证明)
?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,上顶点为
,上顶点为![]() ,
, ![]() 是斜边长为
是斜边长为![]() 的等腰直角三角形,若直线
的等腰直角三角形,若直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
(Ⅲ)是否存在![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x+sin2x,下列结论中错误的是( )
A. f(x)是偶函数
B. 函数f(x)最小值为![]()
C. ![]() 是函数f(x)的一个周期
是函数f(x)的一个周期
D. 函数f(x)在![]() 内是减函数
内是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com