已知函数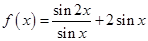
.
（1）求函数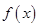
的定义域和最小正周期；
（2）若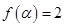
，
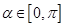，求
的值.
优加精卷系列答案科目：高中数学 来源： 题型：解答题
已知函数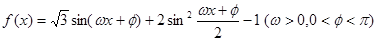
为奇函数，且相邻两对称轴间的距离为
．
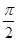（1）当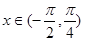
时，求
的单调递减区间；
（2）将函数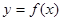
的图象沿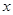
轴方向向右平移
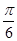个单位长度，再把横坐标缩短到原来的
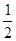（纵坐标不变），得到函数
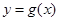的图象．当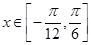
时，求函数
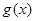的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在已知函数f(x)＝Asin(ωx＋φ)，x∈R(其中A>0，ω>0,0<φ<
)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M(
，－2)．
(1)求f(x)的解析式；
(2)当x∈[
，]时，求f(x)的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图所示，某市政府决定在以政府大楼
为中心，正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地，并考虑与周边环境协调，设计要求该图书馆底面矩形的四个顶点都要在边界上，图书馆的正面要朝市政府大楼.设扇形的半径
，
，
与
之间的夹角为
.
（1）将图书馆底面矩形
的面积
表示成的函数.
（2）求当为何值时，矩形的面积有最大值？其最大值是多少？(用含R的式子表示)
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝sin2ωx＋
sinωxsin
(ω＞0)的最小正周期为
.
(1)写出函数f(x)的单调递增区间；
(2)求函数f(x)在区间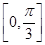
上的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，最小正周期为
；（2）
.
的形式，最后利用周期公式
求函数
的值，进而代数求出
并结合
求出
的值，从而求出
，解得
，
，
的最小正周期为
；
，
且
，
，
；
，
，
，
，又
的周期和单调递增区间；
ABC的三个内角，若AB=1， 
，
，求s1nB的值.
的最大值为3，最小值为
.
的值；
时，函数
的值域.
．
的最小正周期；
上的最大值和最小值.
，钝角
（角
对边为
）的角
满足
.
的单调递增区间；
，求
.