在平面直角坐标系xOy中,已知圆C:x2+y2-(6-2m)x-4my+5m2-6m=0,直线l经过点(1,0).若对任意的实数m,定直线l被圆C截得的弦长为定值,则直线l的方程为________.
2x+y-2=0
分析:根据圆的方程求出圆心和半径,由题意可得圆心C到直线l的距离为定值.当直线l的斜率不存在时,经过检验不
符合条件.当直线l的斜率存在时,直线l的方程为 y-0=k(x-1),圆心C到直线l的距离为定值求得k的值,从而求得
直线l的方程.
解答:圆C:x
2+y
2-(6-2m)x-4my+5m
2-6m=0 即[x-(3-m)]
2+(y-2m)
2=9,表示以C(3-m,2m)为圆心,半径等于3的圆.
∵直线l经过点(1,0),对任意的实数m,定直线l被圆C截得的弦长为定值,则圆心C到直线l的距离为定值.
当直线l的斜率不存在时,直线l的方程为 x=1,圆心C到直线l的距离为|m-3-1|=|m-4|,不是定值.
当直线l的斜率存在时,设直线l的斜率为k,则直线l的方程为 y-0=k(x-1),即 kx-y-k=0.
此时,圆心C到直线l的距离 d=
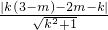
=
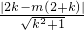
为定值,与m无关,
故 k=-2,故直线l的方程为 y-0=-2(x-1),即 2x+y-2=0,
故答案为 2x+y-2=0.
点评:本题主要考查圆的标准方程,直线和圆的位置关系,点到直线的距离公式,体现了分类讨论的数学思想,属于中档题

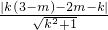 =
=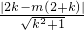 为定值,与m无关,
为定值,与m无关,

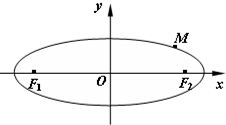 如图,在平面直角坐标系xoy中,已知椭圆C:
如图,在平面直角坐标系xoy中,已知椭圆C: