
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性并指出相应单调区间;
的单调性并指出相应单调区间;
(2)若![]() ,设
,设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,且
,且![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中,将底面为直角三角形且侧棱垂直于底面的三棱柱称之为堑堵;将底面为矩形且一侧棱垂直于底面的四棱锥称之为阳马;将四个面均为直角三角形的四面体称之为鳖臑[biē nào].某学校科学小组为了节约材料,拟依托校园内垂直的两面墙和地面搭建一个堑堵形的封闭的实验室![]() ,
,![]() 是边长为2的正方形.
是边长为2的正方形.


(1)若![]() 是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
是等腰三角形,在图2的网格中(每个小方格都是边长为1的正方形)画出堑堵的三视图;
(2)若![]() ,
,![]() 在
在![]() 上,证明:
上,证明:![]() ,并回答四面体
,并回答四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)当阳马![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:①如果向量![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么![]() 的关系是不共线;②
的关系是不共线;②![]() 为空间四点,且向量
为空间四点,且向量![]() 不构成空间的一个基底,那么点
不构成空间的一个基底,那么点![]() 一定共面;③已知向量
一定共面;③已知向量![]() 是空间的一个基底,则向量
是空间的一个基底,则向量![]() ,也是空间的一个基底。其中正确的命题是( )
,也是空间的一个基底。其中正确的命题是( )
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
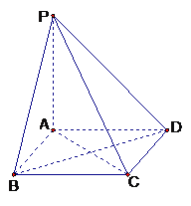
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B余弦值的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形.
都为矩形.
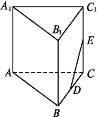
(1)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(2)设![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论.
?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为正实数.
为正实数.
(Ⅰ)若![]() 是函数
是函数![]() 的极值点,讨论函数
的极值点,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() 在
在![]() 上无最小值,且
上无最小值,且![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围,并由此判断曲线
的取值范围,并由此判断曲线![]() 与曲线
与曲线![]() 在
在![]() 交点个数.
交点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
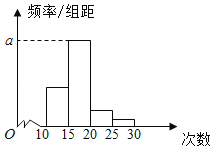
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和![]() .
.
(1)求数列{an}的通项公式an;
(2)设数列{bn}的前n项和为Tn,满足b1=1,![]() .
.
①求数列{bn}的通项公式bn;
②若存在p,q,k∈N*,p<q<k,使得ambq,amanbp,anbk成等差数列,求m+n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com