练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

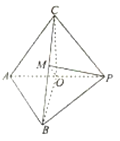
    【题目】如图，在三棱锥中，平面平面，、均为等边三角形，为的中点，点在上.

    （1）求证：平面平面；

    （2）若点是线段的中点，求直线与平面所成角的正弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）证明平面，再利用面面垂直的判定定理，即可证明结论；

    （2）以，，所在的直线分别为，，轴建立空间直角坐标系，设，求出向量和面的一个法向量，再求两向量夹角的余弦值，从而求得答案.

    （1）因为、均为等边三角形，为的中点，

    所以，.

    又，所以平面，即平面.

    又平面，所以平面平面；

    （2）因为平面平面，平面平面，，平面，所以平面.

    又平面，所以，所以，，两两互相垂直.

    故以，，所在的直线分别为，，轴建立空间直角坐标系如下图所示：

    不妨设，则，.

    则点，，，，，.

    则，，，

    设平面的法向量为，则，

    取，，，则，

    ，，，

    ，

    则直线与平面所成角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线:上的点到焦点的距离最小值为1.

    (1)求的值;

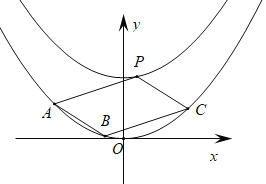
    (2)若点在曲线:上,且在曲线上存在三点,,,使得四边形为平行四边形.求平行四边形的面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校高二年级的第二学期，因某学科的任课教师王老师调动工作，于是更换了另一名教师赵老师继任.第二学期结束后从全学年的该门课的学生考试成绩中用随机抽样的方法抽取了容量为50的样本，用茎叶图表示如下：

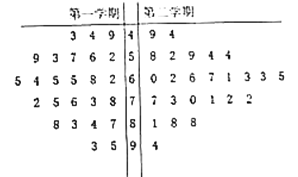
    学校秉持均衡发展、素质教育的办学理念，对教师的教学成绩实行绩效考核，绩效考核方案规定：每个学期的学生成绩中与其中位数相差在范围内（含）的为合格，此时相应的给教师赋分为1分；与中位数之差大于10的为优秀，此时相应的给教师赋分为2分；与中位数之差小于-10的为不合格，此时相应的给教师赋分为-1分.

    （Ⅰ）问王老师和赵老师的教学绩效考核平均成绩哪个大？

    （Ⅱ）是否有的把握认为“学生成绩取得优秀与更换老师有关”.

    附：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着科技的发展，网购已经逐渐融入了人们的生活，在家里不用出门就可以买到自己想要的东西，在网上付款即可，两三天就会送到自己的家门口，所以选择网购的人数在逐年增加.某网店统计了2014年一2018年五年来在该网店的购买人数（单位：人）各年份的数据如下表：

    年份（）

    1

    2

    3

    4

    5

    24

    27

    41

    64

    79

    （1）依据表中给出的数据，是否可用线性回归模型拟合与时间（单位：年）的关系，请通过计算相关系数加以说明，（若，则该线性相关程度很高，可用线性回归模型拟合）

    附：相关系数公式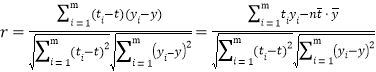

    参考数据

    （2）该网店为了更好的设计2019年的“双十一”网购活动安排，统计了2018年“双十一”期间8个不同地区的网购顾客用于网购的时间x（单位：小时）作为样本，得到下表

    地区

    时间

    0.9

    1.6

    1.4

    2.5

    2.6

    2.4

    3.1

    1.5

    ①求该样本数据的平均数；

    ②通过大量数据统计发现，该活动期间网购时间近似服从正态分布，如果预计2019年“双十一”期间的网购人数大约为50000人，估计网购时间的人数.

    （附：若随机变量服从正态分布则，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

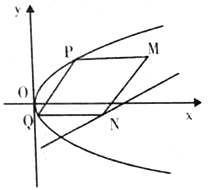
    【题目】抛物线有光学性质，即由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出，反之亦然.如图所示，今有抛物线，一光源在点处，由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点，反射后，又射向抛物线上的点，再反射后又沿平行于抛物线的对称轴方向射出，途中遇到直线上的点，再反射后又射回点.设，两点的坐标分别是，.

    （1）证明：；

    （2）若四边形是平行四边形，且点的坐标为.求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝ax＋(a，b∈Z)，曲线y＝f(x)在点(2，f(2))处的切线方

    程为y＝3.

    (1)求f(x)的解析式；

    (2)证明：曲线y＝f(x)上任一点的切线与直线x＝1和直线y＝x所围三角形的面积为定值，

    并求出此定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校在2019年的冬令营考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下图所示：

    组号

    分组

    频数

    频率

    第1组

    5

    0.050

    第2组

    35

    0.350

    第3组

    10

    0.100

    第4组

    20

    0.200

    第5组

    30

    0.300

    合计

    100

    1.00

    （1）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？

    （2）在（1）的前提下，高校决定在这6名学生中，随机抽取2名学生接受A考官进行面试，求第4组至少有一名学生被A考官测试的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 .

    （1）若是上的增函数，求的取值范围；

    （2）若函数有两个极值点，判断函数零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆与直线相交于、两点，为原点，若.

    （1）求实数的值；

    （2）求的面积.

    查看答案和解析>>

    同步练习册答案