
【题目】设函数![]() ,若存在
,若存在![]() (其中
(其中![]() )
)
(1)求实数![]() 的取值范围,
的取值范围,
(2)证明:![]() .
.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
(1)先利用导数的符号讨论函数的单调性,根据题设条件可得函数的最大值为正,再分![]() 和
和![]() 两种情况讨论,前者无两个不同的零点,后者可利用零点存在定理证明函数有两个零点.
两种情况讨论,前者无两个不同的零点,后者可利用零点存在定理证明函数有两个零点.
(2)根据(1)可把要证明的不等式转化为证明![]() ,根据函数的单调性及
,根据函数的单调性及![]() 可把前者转为
可把前者转为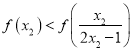 , 构建新函数
, 构建新函数![]()
![]() 可证明该不等式.
可证明该不等式.
解:(1)令![]() ,则
,则![]()
![]() 时,
时,![]() 时;当
时;当![]() ,
,![]() ,
,
![]() 在
在![]() 递增,
递增,![]() 递减,且
递减,且![]() ,
,
由题设,![]() 有两个不同的零点,故
有两个不同的零点,故![]() 即
即![]() .
.
若![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 无零点;
无零点;
而![]() 在
在![]() 递增,故
递增,故![]() 在
在![]() 上至多有一个零点,故
上至多有一个零点,故![]() 不符合;
不符合;
若![]() ,则
,则![]() ,
,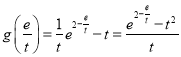 ,
,
考虑![]() ,因为
,因为![]() ,故
,故![]() ,
,
![]() 为
为![]() 上的增函数,故
上的增函数,故![]() 即
即![]() ,
,
因![]() 在
在![]() 递增,
递增,![]() 递减,且
递减,且![]() ,结合零点存在定理可知
,结合零点存在定理可知![]() 有两个不同的零点,故
有两个不同的零点,故![]() .
.
(2)由(1)知:![]() ,
,
要证:![]() 成立,只需证:
成立,只需证:![]() ,
,
![]() 在
在![]() 递增,故只需证:
递增,故只需证: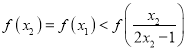
即证![]() .
.
只需证:![]() ,即证:
,即证:![]() .
.
令![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() .证毕
.证毕


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
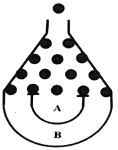
【题目】某超市国庆大酬宾,购物满100元可参加一次游戏抽奖活动,游戏抽奖规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的入口处,小球自由落下过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋得奖金4元,落入B袋得奖金8元,已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
.已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 命题“,使得
命题“,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
④命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
其中所有正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应新高考改革,某校组织了一次新高考质量测评(总分100分),在成绩统计分析中,抽取12名学生的成绩以茎叶图形式表示如图,学校规定测试成绩低于87分的为“未达标”,分数不低于87分的为“达标”.
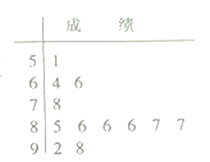
(1)求这组数据的众数和平均数;
(2)在这12名学生中从测试成绩介于80~90之间的学生中任选2人,求至少有1人“达标”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①![]() 越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若
越小,X与Y有关联的可信度越小;②若两个随机变量的线性相关性越强,则相关系数r的值越接近于1;③“若![]() ,则
,则![]() 类比推出,“若
类比推出,“若![]() ,则
,则![]() ;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
;④命题“有些有理数是无限循环小数,整数是有理数,所以整数是无限循环小数”是假命题,推理错误的原因是使用了“三段论”,推理形式错误.其中说法正确的有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中放有大小和形状相同而颜色互不相同的小球若干个, 其中标号为0的小球1个, 标号为1的小球1个, 标号为2的小球2个, 从袋子中不放回地随机抽取2个小球, 记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1) 记事件![]() 表示“
表示“![]() ”, 求事件
”, 求事件![]() 的概率;
的概率;
(2) 在区间![]() 内任取2个实数
内任取2个实数![]() , 记
, 记![]() 的最大值为
的最大值为![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。
(1)求曲线![]() 的极坐标方程和直线l的直角坐标方程;
的极坐标方程和直线l的直角坐标方程;
(2)设直线l与曲线![]() 交于不同的两点A,B,点M为抛物线
交于不同的两点A,B,点M为抛物线![]() 的焦点,求
的焦点,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com