
设函数![]() ,其中
,其中![]() 。
。
(I)解不等式![]() ;
;
(II)证明:当![]()
![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调函数。
上是单调函数。
本小题主要考查不等式的解法、函数的单调性等基本知识,分类讨论的数学思想方法和运算、推理能力.
(Ⅰ)解:不等式f(x)≤1即![]() ≤1+ax,
≤1+ax,
由此得1≤1+ax,即ax≥0,其中常数a>0,
所以,原不等式等价于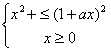 ,
,
即 ![]()
所以,当0<a<1时,所给不等式的解集为{x|0≤x≤![]() };
};
当a≥1时,所给不等式的解集为{x|x≥0}.
(Ⅱ)证明:在区间[0,+∞)上任取x1,x2使得 x1<x2.
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=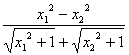 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(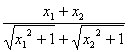 -a).
-a).
∵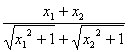 <1,且a≥1,
<1,且a≥1,
∴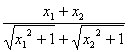 -a<0.
-a<0.
又 x1-x2<0,
∴f(x1)-f(x2)>0,
即 f(x1)>f(x2).
所以,当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.


科目:高中数学 来源:2013-2014学年湖南汝城第一中学、长沙实验中学高三11月联考理数学卷(解析版) 题型:解答题
设函数 ,其中
,其中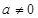 .
.
(I)若函数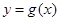 图象恒过定点P,且点P关于直线
图象恒过定点P,且点P关于直线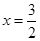 的对称点在
的对称点在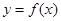 的图象上,求m的值;
的图象上,求m的值;
(Ⅱ)当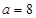 时,设
时,设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅲ)在(I)的条件下,设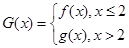 ,曲线
,曲线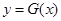 上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
上是否存在两点P、Q,使△OPQ(O为原点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三上学期第一次检测文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
设函数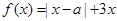 ,其中
,其中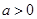 .
.
(I)当a=1时,求不等式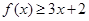 的解集.
的解集.
(II)若不等式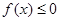 的解集为{x|
的解集为{x|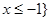 ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源:河北省衡水中学2011-2012学年高三下学期一调考试(数学文) 题型:解答题
选修4-5:不等式选讲
设函数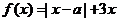 ,其中
,其中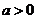 .
.
(I)当a=1时,求不等式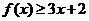 的解集.
的解集.
(II)若不等式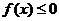 的解集为{x|
的解集为{x|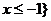 ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com