
【题目】已知函数f(x)=|x﹣1|+|2x﹣6|(x∈R),记f(x)的最小值为c.
(1)求c的值;
(2)若实数ab满足a>0,b>0,a+b=c,求![]() 的最小值.
的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=1,AD=2,点E、F分别在线段AB、AD上,且EF∥CD,将△AEF沿EF折起到△MEF的位置,并使平面MEF⊥平面BCDFE,得到几何体M﹣BCDEF,则折叠后的几何体的体积的最大值为_____.
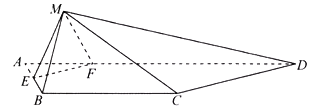
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD﹣A1B1C1D1中,所有棱长均为2,∠AA1D1=∠AA1B1=60°,∠D1A1B1=90°.
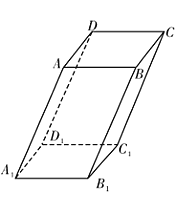
(1)求证:A1C⊥B1D1;
(2)求对角线AC1的长;
(3)求二面角C1﹣AB1﹣D1的平面角的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词,寻文化基因,品生活之美”为宗旨.每一期的比赛包含以下环节:“个人追逐赛”、“攻擂资格争夺赛”和“擂主争霸赛”,其中“擂主争霸赛”由“攻擂资格争夺赛”获胜者与上一场擂主进行比拼.“擂主争霸赛”共有九道抢答题,抢到并答对者得一分,答错则对方得一分,率先获得五分者即为该场擂主.在《中国诗词大会》的某一期节目中,若进行“擂主争霸赛”的甲乙两位选手每道抢答题得到一分的概率都是为0.5,则抢答完七道题后甲成为擂主的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区老年人中,需要志愿帮助的老年人的比例?说明理由.
P | 0.0 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com