Question

17．如图，四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在线段AD上，AG=$\frac{1}{3}$GD，BG⊥GC，BG=GC=2，E是BC的中点，四面体P-BCG的体积为$\frac{8}{3}$．
（1）求异面直线GE与PC所成角的余弦值；
（2）棱PC上是否存在一点F，使DF⊥GC，若存在，求$\frac{PF}{FC}$的值，若不存在，请说明理由．

Answer 1

分析 （1）由已知考查PG，在平面ABCD内，过C点作CH∥EG交AD于H，连结PH，则∠PCH（或其补角）就是异面直线GE与PC所成的角．在△PCH中，由余弦定理即可求得cos∠PCH的值．
（2）在平面ABCD内，过D作DM⊥GC，M为垂足，连结MF，可证FM∥PG，由GM⊥MD得：GM=GD•cos45°=$\frac{3}{2}$，由DF⊥GC，即可求得$\frac{PF}{FC}$的值．

解答 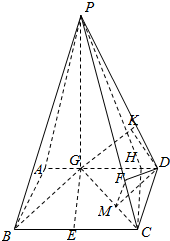解：（1）由已知${V}_{P-BGC}={\frac{1}{3}S}_{△BCG}•PG$=$\frac{1}{3}•\frac{1}{2}BG•GC•PG$=$\frac{8}{3}$，
∴PG=4，
在平面ABCD内，过C点作CH∥EG交AD于H，连结PH，则∠PCH（或其补角）就是异面直线GE与PC所成的角．
在△PCH中，CH=$\sqrt{2}$，PC=$\sqrt{20}$，PH=$\sqrt{18}$，
由余弦定理得，cos∠PCH=$\frac{\sqrt{10}}{10}$．
（2）在平面ABCD内，过D作DM⊥GC，M为垂足，连结MF，又因为DF⊥GC，
∴GC⊥平面MFD，∴GC⊥FM，
由平面PGC⊥平面ABCD，
∴FM⊥平面ABCD，
∴FM∥PG，
由GM⊥MD得：GM=GD•cos45°=$\frac{3}{2}$，
∵$\frac{PF}{FC}=\frac{GM}{MC}=\frac{\frac{3}{2}}{\frac{1}{2}}=3$，
∴由DF⊥GC，可得$\frac{PF}{FC}=3$．

点评 本题主要考查了直线与平面垂直的性质，异面直线及其所成的角，考查了空间想象能力和推理论证能力，属于中档题．