解:(Ⅰ)∵圆心O到直线l:x+y+8=0的距离为
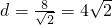
,
∴直线l被圆O截得的弦长为
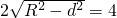
,
∵直线l被圆O截得的弦长与椭圆的长轴长相等,
∴2a=4,∴a=2,
∵椭圆的离心率为e=

,
∴c=

∴b
2=a
2-c
2=1
∴椭圆C的方程为:

; …(4分)
(Ⅱ)∵
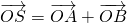
,∴四边形OASB是平行四边形.
假设存在这样的直线l,使四边形OASB的对角线长相等,则四边形OASB为矩形,因此有

,
设A(x
1,y
2),B(x
2,y
2),则x
1x
2+y
1y
2=0.…(7分)
直线l的斜率显然存在,设过点(3,0)的直线l方程为:y=k(x-3),
由
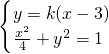
,得(1+4k
2)x
2-24k
2x+36k
2-4=0,
由△=(-24k
2)
2-4(1+4k
2)(36k
2-4)>0,可得-5k
2+1>0,即
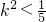
.…(9分)
∴
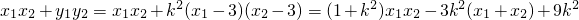
=
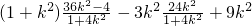
,
由x
1x
2+y
1y
2=0得:
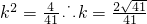
,满足△>0.…(12分)
故存在这样的直线l,其方程为
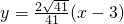
.…(13分)
分析:(Ⅰ)计算圆心O到直线l:x+y+8=0的距离,可得直线l被圆O截得的弦长,利用直线l被圆O截得的弦长与椭圆的长轴长相等,可求a的值,利用椭圆的离心率为e=

,即可求得椭圆C的方程;
(Ⅱ)由
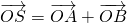
,可得四边形OASB是平行四边形.假设存在这样的直线l,使四边形OASB的对角线长相等,则四边形OASB为矩形,因此有

,设直线方程代入椭圆方程,利用向量的数量积公式,即可求得结论.
点评:本题考查椭圆的标准方程,考查直线与圆、直线与椭圆的位置关系,考查向量知识的运用,联立方程,利用向量的数量积公式、韦达定理是关键.

 =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ,直线l被圆O截得的弦长与椭圆的长轴长相等.
,直线l被圆O截得的弦长与椭圆的长轴长相等.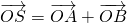 (O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在,求出直线l的方程,若不存在,说明理由.
(O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在,求出直线l的方程,若不存在,说明理由.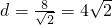 ,
,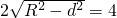 ,
, ,
,
 ; …(4分)
; …(4分)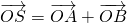 ,∴四边形OASB是平行四边形.
,∴四边形OASB是平行四边形. ,
,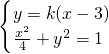 ,得(1+4k2)x2-24k2x+36k2-4=0,
,得(1+4k2)x2-24k2x+36k2-4=0,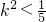 .…(9分)
.…(9分)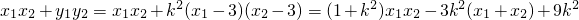 =
=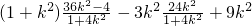 ,
,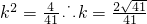 ,满足△>0.…(12分)
,满足△>0.…(12分)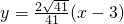 .…(13分)
.…(13分) ,即可求得椭圆C的方程;
,即可求得椭圆C的方程;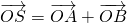 ,可得四边形OASB是平行四边形.假设存在这样的直线l,使四边形OASB的对角线长相等,则四边形OASB为矩形,因此有
,可得四边形OASB是平行四边形.假设存在这样的直线l,使四边形OASB的对角线长相等,则四边形OASB为矩形,因此有 ,设直线方程代入椭圆方程,利用向量的数量积公式,即可求得结论.
,设直线方程代入椭圆方程,利用向量的数量积公式,即可求得结论.
