
【题目】如图所示,A,B,C是双曲线 ![]() =1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是( )
=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是( ) 
A.![]()
B.![]()
C.![]()
D.3
【答案】A
【解析】解:由题意可得在直角三角形ABF中,OF为斜边AB上的中线,即有|AB|=2|OA|=2|OF|=2c,
设A(m,n),则m2+n2=c2 ,
又 ![]() ﹣
﹣ ![]() =1,
=1,
解得m= ![]() ,n=
,n= ![]() ,
,
即有A( ![]() ,
, ![]() ),B(﹣
),B(﹣ ![]() ,﹣
,﹣ ![]() ),
),
又F(c,0),
由于BF⊥AC且|BF|=|CF|,
可设C(x,y),即有 ![]()
![]() =﹣1,
=﹣1,
又(c+ ![]() )2+(
)2+( ![]() )2=(x﹣c)2+y2 ,
)2=(x﹣c)2+y2 ,
可得x= ![]() ,y=﹣
,y=﹣ ![]() ,
,
将C( ![]() ,﹣
,﹣ ![]() )代入双曲线方程,可得
)代入双曲线方程,可得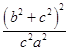 ﹣
﹣ 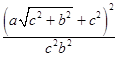 =1,
=1,
化简可得 ![]() (b2﹣a2)=a3 ,
(b2﹣a2)=a3 ,
由b2=c2﹣a2 , e= ![]() ,
,
可得(2e2﹣1)(e2﹣2)2=1,
对照选项,代入检验可得e= ![]() 成立.
成立.
故选:A.


科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发,![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;

(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式:
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.设p:f(x)=x3+2x2+mx+1是R上的单调增函数, ![]() ,则p是q的必要不充分条件
,则p是q的必要不充分条件
B.若命题 ![]() ,则¬p:?x∈R,x2﹣x+1>0
,则¬p:?x∈R,x2﹣x+1>0
C.奇函数f(x)定义域为R,且f(x﹣1)=﹣f(x),那么f(8)=0
D.命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0,则x2+y2≠0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是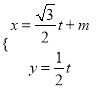 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式|x+a|≤b的解集为[﹣6,2].
(1)求实数a,b的值;
(2)若实数m,n满足|am+n|< ![]() ,|m﹣bn|<
,|m﹣bn|< ![]() ,求证:|n|<
,求证:|n|< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+ax(a∈R).
(Ⅰ)当a=0,求f(x)的最小值;
(Ⅱ)若函数g(x)=f(x)+lnx在区间[1,+∞)上为增函数,求实数a的取值范围;
(Ⅲ)过点P(1,﹣3)恰好能作函数y=f(x)图象的两条切线,并且两切线的倾斜角互补,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣1|+x2﹣kx.
(1)若k=2时,求出函数f(x)的单调区间及最小值;
(2)若f(x)≥0恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com