
如图:A、B是两个定点,且|AB|=2,动点M到A点的距离是4,线段MB的垂直平分线l交MA于点P,直线k垂直于直线AB,且B点到直线k的距离为3.
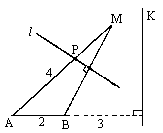
(Ⅰ)建立适当的坐标系,求动点P的轨迹方程;
(Ⅱ)求证:点P到点B的距离与点P到直线k的距离之比为定值;
(Ⅲ)(理)若点P到A、B两点的距离之积为m,当m取最大值时,求P点的坐标.
|
(Ⅰ)解:以直线AB为x轴,AB的中点为原点建立直角坐标系,则点A,B的坐标分别是(-1,0),(1,0). ∵l为MB的垂直平分线,
∴|PM|=|PB|,|PA|+|PB|=|PA|+|PM|=4. ∴P点的轨迹是以A,B为两个焦点,长轴长为4的椭圆,其方程是: (Ⅱ)证明:∵椭圆的右准线方程是x=4恰为直线k的方程.根据椭圆的定义知点P到点B的距离与点P到直线k的距离之比为离心率e= (Ⅲ)解:m=|PA|·|PB|≤ |


科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
如图所示,设C(a,b)是定点(ab≠0),过C作两条互相垂直的直线l1和l2,且l1,l2分别交x,y轴于A,B,求:
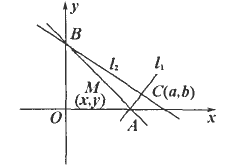
(1)线段AB中点M的轨迹方程;
(2)|MC|的最小值.
查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图,矩形ABCD的两个顶点A,B在x轴上,另两个顶点C,D在抛物线y=4-x2位于x轴上方的曲线上,求矩形ABCD的面积最大值.

查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
如图,一载着重危病人的火车从O地出发,沿射线OA行驶,其中tanα=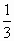 ,在距离O地5a(a为正数)公里北偏东β角的N处住有一位医学专家,其中sinβ=
,在距离O地5a(a为正数)公里北偏东β角的N处住有一位医学专家,其中sinβ=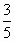 ,现110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车,并在C处相遇,经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时,抢救最及时,
,现110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车,并在C处相遇,经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时,抢救最及时,
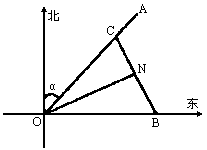
(1)求S关于p的函数关系;
(2)当p为何值时,抢救最及时.
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:047
如图所示,已知矩形ABCD中,AB=1,BC=a(a>0),PA⊥面ABCD.
(1)问BC边上是否存在点Q,使得PQ⊥QD,并说明理由.
(2)若PA=1,且BC边上有且只有一点Q,使得PQ⊥QD.求这时二面角Q-PD-A的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com