
【题目】如图,OA是南北方向的一条公路,OB是北偏东45°方向的一条公路,某风景区的一段边界为曲线C.为方便游客光,拟过曲线C上的某点分别修建与公路OA,OB垂直的两条道路PM,PN,且PM,PN的造价分别为5万元/百米,40万元/百米,建立如图所示的直角坐标系xoy,则曲线符合函数y=x+ ![]() (1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.
(1≤x≤9)模型,设PM=x,修建两条道路PM,PN的总造价为f(x)万元,题中所涉及的长度单位均为百米.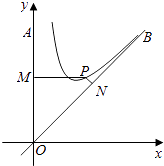
(1)求f(x)解析式;
(2)当x为多少时,总造价f(x)最低?并求出最低造价.
【答案】
(1)解:在如图所示的直角坐标系中,因为曲线C的方程为 ![]() ,
,
所以点P坐标为 ![]() ,
,
直线OB的方程为x﹣y=0,
则点P到直线x﹣y=0的距离为 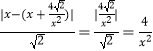 ,
,
又PM的造价为5万元/百米,PN的造价为40万元/百米.
则两条道路总造价为 ![]() .
.
答:两条道路PM,PN总造价f(x)为 ![]() (1≤x≤9);
(1≤x≤9);
(2)因为 ![]() ,
,
所以 ![]() ,
,
令f'(x)=0,得x=4,列表如下:
x | (1,4) | 4 | (4,9) |
f'(x) | ﹣ | 0 | ﹣ |
f(x) | 单调递减 | 极小值 | 单调递增 |
所以当x=4时,函数f(x)有最小值,最小值为 ![]() .
.
答:当x=4时,总造价最低,最低造价为30万元.
【解析】(1)由题意求出点P的坐标以及直线OB的方程根据点到直线的距离公式即可求出f(x)解析式。(2)利用导函数求出极值即为最低造价。


科目:高中数学 来源: 题型:
【题目】已知奇函数y=f(x)定义域是R,当x≥0时,f(x)=x(1﹣x).
(1)求出函数y=f(x)的解析式;
(2)写出函数y=f(x)的单调递增区间.(不用证明,只需直接写出递增区间即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线 ![]() 是函数f(x)=sinx+acosx的图象的一条对称轴.
是函数f(x)=sinx+acosx的图象的一条对称轴.
(1)求函数f(x)的最大值及取得最大值时x的值;
(2)求函数f(x)在[0,π]上的减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若 ![]() ,其中m,n∈R.则m+n的取值范围是( )
,其中m,n∈R.则m+n的取值范围是( )
A.(0,1)
B.(﹣1,0)
C.(1,+∞)
D.(﹣∞,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e|x| , 将函数f(x)的图象向右平移3个单位后,再向上平移2个单位,得到函数g(x)的图象,函数h(x)= ![]() 若对于任意的x∈[3,λ](λ>3),都有h(x)≥g(x),则实数λ的最大值为 .
若对于任意的x∈[3,λ](λ>3),都有h(x)≥g(x),则实数λ的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=BC,点M为棱A1B1的中点.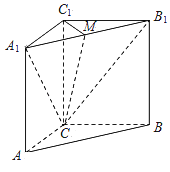
求证:
(1)AB∥平面A1B1C;
(2)平面C1CM⊥平面A1B1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明设置的手机开机密码若连续3次输入错误,则手机被锁定,5分钟后,方可重新输入.某日,小明忘记了开机密码,但可以确定正确的密码是他常用的4个密码之一,于是,他决定逐个(不重复)进行尝试.
(1)求手机被锁定的概率;
(2)设第X次输入后能成功开机,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设圆的方程为(x+2 ![]() )2+y2=48,F1是圆心,F2(2
)2+y2=48,F1是圆心,F2(2 ![]() ,0)是圆内一点,E为圆周上任一点,线EF2的垂直平分线EF1的连线交于P点,设动点P的轨迹为曲线C.
,0)是圆内一点,E为圆周上任一点,线EF2的垂直平分线EF1的连线交于P点,设动点P的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设直线l(与x轴不重合)与曲线C交于A、B两点,与x轴交于点M.
(i)是否存在定点M,使得 ![]() +
+ ![]() 为定值,若存在,求出点M坐标及定值;若不存在,请说明理由;
为定值,若存在,求出点M坐标及定值;若不存在,请说明理由;
(ii)在满足(i)的条件下,连接并延长AO交曲线C于点Q,试求△ABQ面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com