
【题目】某避暑山庄拟对一个半径为1百米的圆形地块(如图)进行改造,拟在该地块上修建一个等腰梯形![]() ,其中
,其中![]() ,
,![]() ,圆心
,圆心![]() 在梯形内部,设
在梯形内部,设![]() .当该游泳池的面积与周长之比最大时为“最佳游泳池”.
.当该游泳池的面积与周长之比最大时为“最佳游泳池”.

(1)求梯形游泳池的面积![]() 关于
关于![]() 的函数关系式,并指明定义域;
的函数关系式,并指明定义域;
(2)求当该游泳池为“最佳游泳池”时![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以椭圆长、短轴四个端点为顶点为四边形的面积为
,以椭圆长、短轴四个端点为顶点为四边形的面积为![]() .
.
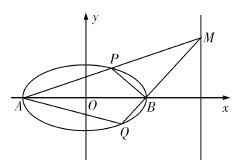
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)如图所示,记椭圆的左、右顶点分别为![]() 、
、![]() ,当动点
,当动点![]() 在定直线
在定直线![]() 上运动时,直线
上运动时,直线![]() 分别交椭圆于两点
分别交椭圆于两点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了200名用户,得到用户的满意度评分,现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 |
|
|
|
|
|
频数 | 12 | 28 | 68 |
| 40 |
频率 | 0.06 |
| 0.34 |
| 0.2 |
(1)求表格中的![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计用户的满意度评分的平均数;
(3)若从这200名用户中随机抽取50人,估计满意度评分高于6分的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]() 、
、![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左,右顶点分别为
)的左,右顶点分别为![]() ,
,![]() ,长轴长为
,长轴长为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为椭圆
为椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,证明:直线
的任意一点,证明:直线![]() ,
,![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)已知两条互相垂直的直线![]() ,
,![]() 都经过椭圆
都经过椭圆![]() 的右焦点
的右焦点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
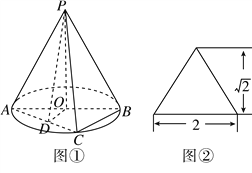
【题目】圆锥![]() 如图①所示,图②是它的正(主)视图.已知圆
如图①所示,图②是它的正(主)视图.已知圆![]() 的直径为
的直径为![]() ,
, ![]() 是圆周上异于
是圆周上异于![]() 的一点,
的一点, ![]() 为
为![]() 的中点.
的中点.
(I)求该圆锥的侧面积S;
(II)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱锥![]() 中,求点
中,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数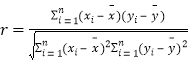 ,
,
回归方程![]() 中,
中,![]()
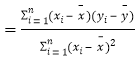 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”.广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极鱼”.已知![]() 或
或 ,下列命题中:①
,下列命题中:①![]() 在平面直角坐标系中表示的区域的面积为
在平面直角坐标系中表示的区域的面积为![]() ;②
;②![]() ,使得
,使得![]() ;③
;③![]() ,都有
,都有![]() 成立;④设点
成立;④设点![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .其中真命题的个数为( )
.其中真命题的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
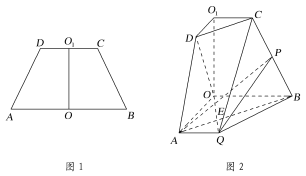
【题目】如图![]() ,在高为
,在高为![]() 的等腰梯形
的等腰梯形![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,将它沿对称轴
,将它沿对称轴![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图
,如图![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上(不同于
上(不同于![]() ,
,![]() 两点),连接
两点),连接![]() 并延长至点
并延长至点![]() ,使
,使![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com