
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若直线![]() 与曲线
与曲线![]() 的交点的横坐标为
的交点的横坐标为![]() ,且
,且![]() ,求整数
,求整数![]() 所有可能的值.
所有可能的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:
(1)求出导函数![]() ,根据
,根据![]() 的值分下、负、0进行讨论,可得
的值分下、负、0进行讨论,可得![]() 的正负,从而得单调性;
的正负,从而得单调性;
(2)![]() 即方程
即方程![]() 的解,由于
的解,由于![]() ,方程变形为
,方程变形为![]() ,这样只要研究函数
,这样只要研究函数![]() 的零点可能在哪个区间即可,由导数知
的零点可能在哪个区间即可,由导数知![]() 是
是![]() 和
和![]() 上的单调增函数,计算
上的单调增函数,计算![]() 可得结论.
可得结论.
试题解析:
(1)解: ![]() ,∴
,∴![]() ,
,
①若![]() 时,
时, ![]() 在
在![]() 上恒成立,所以函数
上恒成立,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
②若![]() 时,当
时,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减;
单调递减;
③若![]() 时,当
时,当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增.
单调递增.
综上,若![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
若![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,在区间
内单调递减,在区间![]() 内单调递增;
内单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内单调递增,在区间
内单调递增,在区间![]() 内单调递减,
内单调递减,
(2)由题可知,原命题等价于方程![]() 在
在![]() 上有解,
上有解,
由于![]() ,所以
,所以![]() 不是方程的解,
不是方程的解,
所以原方程等价于![]() ,令
,令![]() ,
,
因为![]() 对于
对于![]() 恒成立,
恒成立,
所以![]() 在
在![]() 和
和![]() 内单调递增.
内单调递增.
又![]() ,
,
所以直线![]() 与曲线
与曲线![]() 的交点有两个,
的交点有两个,
且两交点的横坐标分别在区间![]() 和
和![]() 内,
内,
所以整数![]() 的所有值为-3,1.
的所有值为-3,1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程 ![]() 恒过样本中心(
恒过样本中心( ![]() ,
, ![]() ),且至少过一个样本点;
),且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)若直线![]() 过焦点
过焦点![]() ,且与圆
,且与圆![]() 交于
交于![]() (其中
(其中![]() 在
在![]() 轴同侧),求证:
轴同侧),求证: ![]() 是定值;
是定值;
(Ⅱ)设抛物线![]() 在
在![]() 和
和![]() 点的切线交于点
点的切线交于点![]() ,试问:
,试问: ![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为菱形?若存在,请说明理由并求此时直线
为菱形?若存在,请说明理由并求此时直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+b(a>0)在区间[﹣1,4]上有最大值10和最小值1.设g(x)= ![]() .
.
(1)求a、b的值;
(2)证明:函数g(x)在[ ![]() ,+∞)上是增函数;
,+∞)上是增函数;
(3)若不等式g(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数g(x)= ![]() 的定义域是( )
的定义域是( )
A.[0,1)∪(1,2]
B.[0,1)∪(1,4]
C.[0,1)
D.(1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出的样本频率分布直方图如图,那么在这片树木中底部周长大于100cm的株树大约中( ) 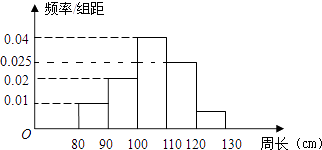
A.3000
B.6000
C.7000
D.8000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若f(x)在区间(﹣∞,2],上是减函数,且对任意的x1 , x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com