
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,圆
,圆![]() :
:![]() .
.
(Ⅰ)求![]() 的取值范围,并求出圆心坐标;
的取值范围,并求出圆心坐标;
(Ⅱ)若圆![]() 的半径为1,过点
的半径为1,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅲ)有一动圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上,若动圆
上,若动圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 的取值范围为
的取值范围为![]() ,圆心
,圆心![]() 坐标为
坐标为![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)把圆的方程配成标准式,方程右边需大于零,即可求得参数![]() 的取值范围。
的取值范围。
(Ⅱ)已知圆![]() 的圆心坐标为
的圆心坐标为![]() ,当半径为1时,可求得圆的标准方程;用待定系数法求过圆外一点的切线方程,分析直线的斜率存在与否,如存在设斜率为
,当半径为1时,可求得圆的标准方程;用待定系数法求过圆外一点的切线方程,分析直线的斜率存在与否,如存在设斜率为![]() ,利用圆心到直线的距离等于半径即可得到方程,解得
,利用圆心到直线的距离等于半径即可得到方程,解得![]() .
.
(Ⅲ)设出圆心![]() 的坐标,表示出圆的方程,进而根据
的坐标,表示出圆的方程,进而根据![]() ,点
,点![]() 在
在![]() 的中垂线上,由
的中垂线上,由![]() 坐标已知,从而可求
坐标已知,从而可求![]() 的中垂线方程,根据
的中垂线方程,根据![]() 在圆上,进而确定不等式关系求得
在圆上,进而确定不等式关系求得![]() 的范围.
的范围.
(Ⅰ) ![]() 化为
化为![]()
由![]() ,∴
,∴ ![]() 的取值范围为
的取值范围为![]() ,圆心
,圆心![]() 坐标为
坐标为![]()
(Ⅱ)由(Ⅰ)知圆![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,当半径为1时,
,当半径为1时,
圆![]() 的方程为:
的方程为: ![]() 将
将![]() 代入
代入![]()
得![]() ,∴
,∴![]() 在圆
在圆![]() 外,
外,
设所求圆![]() 的切线方程为
的切线方程为![]() ,∴
,∴![]()
∴![]() ∴
∴![]()
∴![]() ∴所求圆
∴所求圆![]() 的切线方程为:
的切线方程为: ![]()
即![]() .
.
(Ⅲ)∵圆![]() 的圆心在直线
的圆心在直线![]() 上,所以,设圆心
上,所以,设圆心![]()
![]() ,又半径为1,
,又半径为1,
则圆![]() 的方程为:
的方程为: ![]() ,
,
又∵![]() ,
,
∴点![]() 在
在![]() 的中垂线
的中垂线![]() 上,
上,![]() 的中点
的中点![]() 得直线
得直线![]() :
: ![]()
∴点![]() 应该既在圆
应该既在圆![]() 上又在直线
上又在直线![]() 上,即:圆
上,即:圆![]() 和直线
和直线![]() 有公共点
有公共点
∴ ![]() ,∴
,∴![]() 终上所述,
终上所述, ![]() 的取值范围为:
的取值范围为: ![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程):
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知射线θ= ![]() 与曲线
与曲线 ![]() (t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 .
(t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值.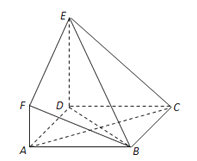
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com