
| A. | f($\frac{3}{4}$)<f($\frac{1}{2}$) | B. | f($\frac{3}{4}$)>f($\frac{1}{2}$) | ||
| C. | f($\frac{3}{4}$)=f($\frac{1}{2}$) | D. | f($\frac{3}{4}$)与f($\frac{1}{2}$)的大小不确定 |
分析 根据条件便可得到$f(\frac{3}{4})=-f(-\frac{11}{4}),f(\frac{1}{2})=-f(-\frac{5}{2})$,而根据f(x)在(-3,-2)上单调递减便可得出$f(-\frac{11}{4})>f(-\frac{5}{2})$,这样便可得出$f(\frac{3}{4})$与$f(\frac{1}{2})$的大小关系.
解答 解:f(x+2)=f(x);
又f(x)为奇函数;
∴$f(\frac{3}{4})=f(\frac{3}{4}+2)=-f(-\frac{11}{4})$,$f(\frac{1}{2})=f(\frac{1}{2}+2)=-f(-\frac{5}{2})$;
$-\frac{11}{4},-\frac{5}{2}∈(-3,-2)$,且$-\frac{11}{4}<-\frac{5}{2}$,f(x)在(-3,-2)上单调递减;
∴$f(-\frac{11}{4})>f(-\frac{5}{2})$;
∴$-f(-\frac{11}{4})<-f(-\frac{5}{2})$;
∴$f(\frac{3}{4})<f(\frac{1}{2})$.
故选:A.
点评 考查奇函数、周期函数的定义,以及减函数的定义,根据减函数的定义比较两个函数值大小的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-$\frac{a}{2}$<x<a} | B. | {x|x>0或x$<-\frac{3}{5}$a} | ||
| C. | {x|-a≤x≤-$\frac{3}{5}$a或0≤x<a} | D. | {x|0<x≤a} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
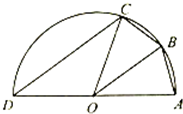 如图所示,AD是半径为5的半圆O的直径,B,C是半圆O上的两点,cos∠AOB=$\frac{4}{5}$,AB=BC,
如图所示,AD是半径为5的半圆O的直径,B,C是半圆O上的两点,cos∠AOB=$\frac{4}{5}$,AB=BC,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2<x<3} | B. | {x|1<x<3} | C. | {x|3<x<4} | D. | {x|1<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 |
| A. | 点(2,3) | B. | 点(3,5) | C. | 点(2.5,4) | D. | 点(2.5,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 12 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com