
 ,
,  .…………………………3分
.…………………………3分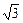 ,OE=
,OE= ,
, 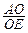 =2,cos∠AEO=
=2,cos∠AEO=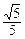 ,
,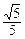 .……………………8分
.……………………8分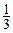 S
S △ACD·h—=
△ACD·h—=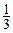 S△OCD·AO.
S△OCD·AO.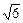 ,
, 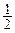
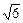 ·
·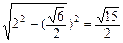 .
.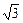 ,S△OCD=
,S△OCD= ,
,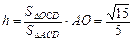 ,
,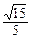 .…………………………12分
.…………………………12分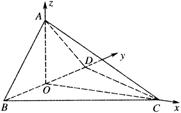
 …………5分
…………5分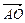 =(0,0,
=(0,0,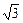 )…………6分
)…………6分 =(0,-1,-
=(0,-1,-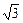 ),
),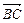 =(
=(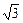 ,1,0).
,1,0).
|
|

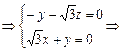 n=(1,-
n=(1,-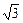 ,1).
,1).
|
|
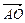 的夹角为
的夹角为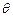 ,则|cos
,则|cos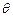 |=
|=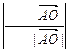 =
=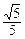 ,
,  ∴二面角A—BC—D的余弦值为
∴二面角A—BC—D的余弦值为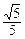 .…………………………8分
.…………………………8分
|
|
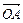 与m的夹角为
与m的夹角为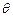 ,则|cos
,则|cos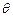 |=
|=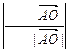 =
=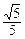 . 设点O到平面ACD的距离为h,
. 设点O到平面ACD的距离为h,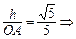 h=
h=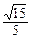 ,
,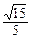 .…………………………12分
.…………………………12分

科目:高中数学 来源:不详 题型:解答题
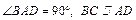 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.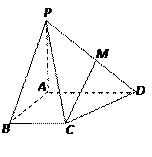
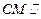 平面PAB;
平面PAB;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
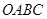 的三条棱
的三条棱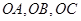 两两垂直,
两两垂直,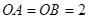 ,
,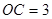 ,
,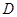 为四面体
为四面体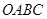 外一点.给出下列命题.
外一点.给出下列命题.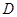 ,使四面体
,使四面体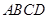 有三个面是直角三角形
有三个面是直角三角形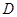 ,使四面体
,使四面体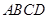 是正三棱锥
是正三棱锥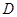 ,使
,使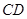 与
与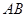 垂直并且相等
垂直并且相等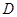 ,使点
,使点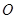 在四面体
在四面体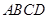 的外接球面上
的外接球面上| A.①② |
| B.②③ |
| C.③ |
| D.③④ |
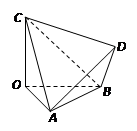
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
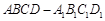 中,棱长都相等;条件乙:直四棱柱
中,棱长都相等;条件乙:直四棱柱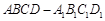 是正方体,那么甲是乙的 ( )
是正方体,那么甲是乙的 ( )| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
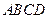 的边长为
的边长为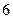 ,
,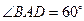 ,
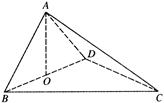
,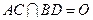 .将菱形
.将菱形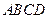 沿对角线
沿对角线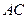 折起,使
折起,使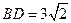 ,得到三棱锥
,得到三棱锥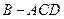 .
.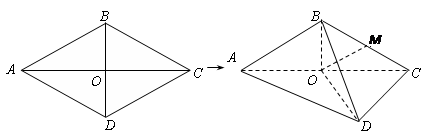
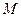 是棱
是棱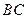 的中点,求证:
的中点,求证: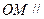 平面
平面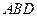 ;
;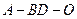 的余弦值;
的余弦值;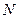 是线段
是线段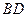 上一个动点,试确定
上一个动点,试确定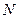 点的位置,使得
点的位置,使得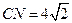 ,并证明你的结论.
,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
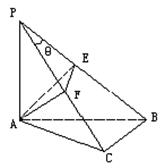
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD=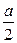 ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .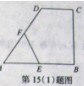
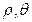 )
)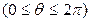 中,曲线
中,曲线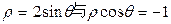 的交点的极坐标为 .
的交点的极坐标为 .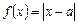 .若不等式
.若不等式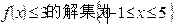 ,则实数
,则实数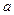 的值为 .
的值为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
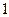 条直线把平面分成
条直线把平面分成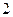 部分;
部分;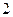 条直线把平面分成
条直线把平面分成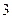 或
或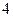 部分;
部分;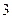 条直线把平面分成
条直线把平面分成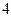 或
或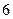 或
或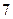 部分。类比空间
部分。类比空间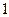 个平面把空间分成 部分;
个平面把空间分成 部分;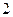 个平面把空间分成 部分;
个平面把空间分成 部分;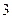 个平面把空间分成 部分。
个平面把空间分成 部分。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com