
【题目】已知函数![]() .
.
(1)若![]() ,解不等式
,解不等式![]() ;
;
(2)关于![]() 的不等式
的不等式![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】设![]() 和
和![]() 是双曲线
是双曲线![]() 上的两点,线段
上的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 不经过坐标原点
不经过坐标原点![]() .
.
(1)若直线![]() 和直线
和直线![]() 的斜率都存在且分别为
的斜率都存在且分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(2)若双曲线的焦点分别为![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求由四点
,求由四点![]() 、
、![]() 、
、![]() 、
、![]() 所围成四边形
所围成四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,O为线段AC上一点,平面ADC⊥平面ABC,且△ADO,△ABO为等腰直角三角形,斜边AO=4![]() .
.
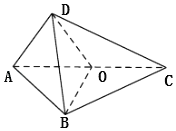
(Ⅰ)求证:AC⊥BD;
(Ⅱ)将△BDO绕DO旋转一周,求所得旋转体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛请自以为来自X星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题;然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答的题目则跳过(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答题),这样所有的题目均有作答,设这位选手可能的答题次序有n种,则n的值为( )
A.512B.511C.1024D.1023
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() ,
,![]() 轴被曲线
轴被曲线![]() 截得的线段长等于C1的长半轴长.
截得的线段长等于C1的长半轴长.
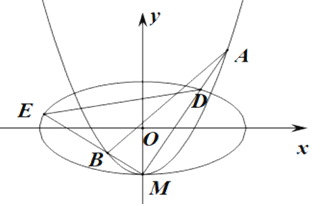
(1)求实数b的值;
(2)设C2与![]() 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线![]() 与C2相交于点A、B,直线MA、MB分别与C1交于点D、E.
与C2相交于点A、B,直线MA、MB分别与C1交于点D、E.
①证明:![]() ;
;
②记△MAB,△MDE的面积分别是![]() 若
若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
(1)![]() 是
是![]() 的极小值点;
的极小值点;
(2)函数![]() 有且只有1个零点;
有且只有1个零点;
(3)![]() 恒成立;
恒成立;
(4)设函数![]() ,若存在区间
,若存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,则
,则![]() .
.
A.(1) (2)B.(2)(4)C.(1) (2) (4)D.(1)(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
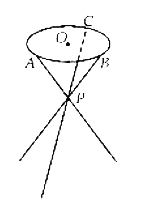
【题目】如图,小凳凳面为圆形,凳脚为三根细钢管.考虑到钢管的受力等因素,设计的小凳应满足:三根细钢管相交处的节点![]() 与凳面圆形的圆心
与凳面圆形的圆心![]() 的连线垂直于凳面和地面,且
的连线垂直于凳面和地面,且![]() 分细钢管上下两段的比值为
分细钢管上下两段的比值为![]() ,三只凳脚与地面所成的角均为
,三只凳脚与地面所成的角均为![]() .若
.若![]() 、
、![]() 、
、![]() 是凳面圆周的三等分点,
是凳面圆周的三等分点,![]() 厘米,求凳子的高度
厘米,求凳子的高度![]() 及三根细钢管的总长度(精确到
及三根细钢管的总长度(精确到![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com