
有四个命题:
①若
p=xa+yb,则p与a、b共面;②若
p与a、b共面,则p=xa+yb;③若
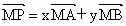 ,则P、M、A、B共面;
,则P、M、A、B共面;
④若
P、M、A、B共面,则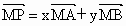 .
.
其中真命题的个数是
[
]|
A .1 |
B .2 |
C .3 |
D .4 |
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| lim |
| x→1 |
| x2+b |
| x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OM |
| 1 |
| 3 |
| AO |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| x2 |
| 9 |
| y2 |
| 16 |
| PF1 |
| PF2 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 9-k |
| y2 |
| 25-k |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| OM |
| 1 |
| 3 |
| AO |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| x2 |
| 9 |
| y2 |
| 16 |
| PF1 |
| PF2 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 9-k |
| y2 |
| 25-k |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建师大附中高二(上)期末数学试卷(理科)(解析版) 题型:填空题
 =
=
 +
+
 +
+
 ,则点M与点A、B、C共面;
,则点M与点A、B、C共面; -
-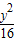 =1的两焦点为F1、F2,点P为双曲线上一点,且
=1的两焦点为F1、F2,点P为双曲线上一点,且 •
• =0,则△PF1F2的面积为16;
=0,则△PF1F2的面积为16; +
+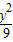 =1与曲线
=1与曲线 +
+ =1(0<k<9)有相同的焦点;
=1(0<k<9)有相同的焦点;查看答案和解析>>
科目:高中数学 来源:2010年高考数学综合训练试卷(04)(解析版) 题型:解答题
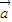 ,
,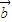 为一平面内两非零向量,则
为一平面内两非零向量,则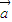 ⊥
⊥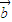 是|
是|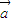 +
+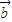 |=|
|=|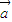 -
-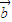 |的充要条件;
|的充要条件;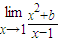 =2,则b=-1.
=2,则b=-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com