设直线x="t" 与函数
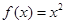
,
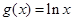
的图像分别交于点M,N,则当
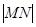
为最小时t的值为
解:设函数y=f(x)-g(x)=x
2-lnx(x>0),求导数得y′=2x-
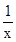
(x>0)
令y′<0,则函数在(0,

)上为单调减函数,令y′>0,则函数在(

,+∞)上为单调增函数,
所以当x=

时,函数取得最小值为
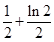
,所以当MN达到最小时t的值为

,选D
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题满分12分) 设函数
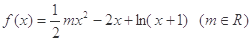
.
(Ⅰ)判断
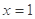
能否为函数
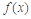
的极值点,并说明理由;
(Ⅱ)若存在
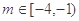
,使得定义在
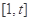
上的函数
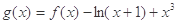
在
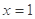
处取得最大值,求实数
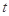
的最大值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
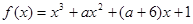
既有极大值又有极小值,则
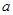
的取值范围为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
本小题满分12分)
设函数

在

及

时取得极值.
(Ⅰ)求a、b的值(6分);
(Ⅱ)若对于任意的

,都有
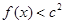
成立,求c的取值范围(6分)
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分15分)设函数
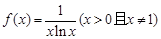
.
(Ⅰ)求函数
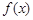
的单调区间;
(Ⅱ)已知
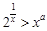
对任意
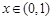
成立,求实数
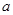
的取值范围;
(Ⅲ)试讨论方程
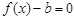
的零点个数.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知非零向量
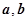
满足:
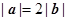
,若函数
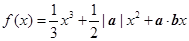
在
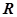
上有极值,设向量
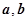
的夹角为
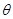
,则
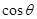
的取值范围为( )
查看答案和解析>>

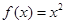 ,
, 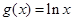 的图像分别交于点M,N,则当
的图像分别交于点M,N,则当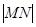 为最小时t的值为
为最小时t的值为


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案