
【题目】如图1,在![]() 中,
中, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
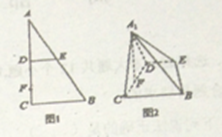
(1)求证: ![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?说明理由.
?说明理由.
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应关系:
x/百万元 | 2 | 4 | 5 | 6 | 8 |
y/百万元 | 30 | 40 | 60 | 50 | 70 |
(1)假定y与x之间有线性相关关系,求其回归直线方程;
(2)若实际的销售额不少于60百万元,则广告费支出应不少于多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
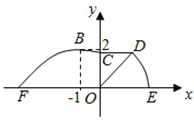
(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电商中“猫狗大战”在节日期间的竞争异常激烈,在刚过去的618全民年中购物节中,某东当日交易额达1195亿元,现从该电商“剁手党”中随机抽取100名顾客进行回访,按顾客的年龄分成了6组,得到如下所示的频率直方图. 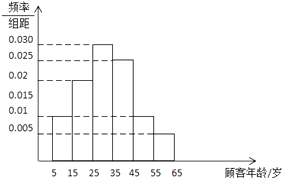
(1)求顾客年龄的众数,中位数,平均数(每一组数据用中点做代表);
(2)用样本数据的频率估计总体分布中的概率,则从全部顾客中任取3人,记随机变量X为顾客中年龄小于25岁的人数,求随机变量X的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值 ![]() 的概率均为
的概率均为 ![]() ,随机变量Y取值
,随机变量Y取值 ![]() 的概率也均为
的概率也均为 ![]() ,比较DX与DY大小关系.
,比较DX与DY大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系 ![]() 中,过椭圆
中,过椭圆 ![]() :
: ![]() (
( ![]() )右焦点的直线
)右焦点的直线 ![]() 交
交 ![]() 于
于 ![]() ,
, ![]() 两点,
两点, ![]() 为
为 ![]() 的中点,且
的中点,且 ![]() 的斜率为
的斜率为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ) ![]() ,
, ![]() 为
为 ![]() 上的两点,若四边形
上的两点,若四边形 ![]() . 的对角线
. 的对角线 ![]() ,求四边形
,求四边形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点. 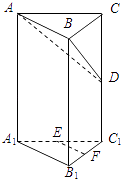
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com