
【题目】给出以下四个结论:
①函数![]() 是偶函数;
是偶函数;
②当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
③若扇形的周长为![]() ,圆心角为
,圆心角为![]() ,则该扇形的弧长为6cm;
,则该扇形的弧长为6cm;
④已知定义域为![]() 的函数
的函数![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
⑤函数![]() 的最小正周期是
的最小正周期是![]()
则上述结论中正确的是______(写出所有正确结论的序号)
【答案】②④
【解析】
利用特殊值代入①中的解析式即可判断①;根据函数单调性及自变量取值范围,可判断②;根据扇形的周长及圆心角即可求得半径,进而求得弧长,可判断③;讨论sinx﹣cosx的符号去绝对值,即可判断④;利用周期性定义验证![]() ,即可判断⑤.
,即可判断⑤.
解:当x![]() 与x
与x![]() 时,代入①中的解析式所得函数值不相等,所以①错误;
时,代入①中的解析式所得函数值不相等,所以①错误;
当x∈[0,![]() ]时,2x
]时,2x![]() x∈[
x∈[![]() ,
,![]() ],
],
由余弦函数图象可知函数f(x)=2cos(2x![]() )的值域是[﹣2,
)的值域是[﹣2,![]() ];所以②正确;
];所以②正确;
因为若扇形的周长为15cm,圆心角为![]() rad,设半径为r,
rad,设半径为r,
则15﹣2r![]() r,解得r=6,所以弧长为l=ar=3 cm,所以③错误;
r,解得r=6,所以弧长为l=ar=3 cm,所以③错误;
当sinx﹣cosx≥0时,函数f(x)![]() cosx,
cosx,
2kπ<x<2kπ![]() (k∈Z)时,f(x)>0;
(k∈Z)时,f(x)>0;
当sinx﹣cosx<0时,函数f(x)![]() sinx,
sinx,
2kπ<x<2kπ![]() (k∈Z)时,f(x)>0,所以④正确.
(k∈Z)时,f(x)>0,所以④正确.
记![]() ,
,![]() ,
,
![]() ,
,
![]() ,故
,故![]() 也是函数的周期,故⑤错误,
也是函数的周期,故⑤错误,
综上所述,②④正确.
故答案为:②④.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
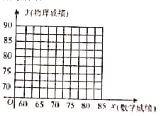
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中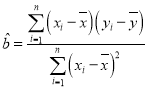 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.

(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若二面角
)若二面角![]() 为直二面角,
为直二面角,
(i)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
(ii)棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某民营企业生产A,B两种产品,根据市场调查与预测,A产品的利润y与投资x成正比,其关系如图甲,B产品的利润y与投资x的算术平方根成正比,其关系如图乙![]() 注:利润与投资单位为万元
注:利润与投资单位为万元![]()

![]() 分别将A,B两种产品的利润y表示为投资x的函数关系式;
分别将A,B两种产品的利润y表示为投资x的函数关系式;
![]() 该企业已筹集到10万元资金,并全部投入A,B两种产品的生产
该企业已筹集到10万元资金,并全部投入A,B两种产品的生产![]() 问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

图1 图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点![]() 作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
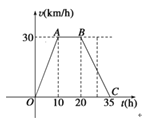
(1)当![]() 时,求s的值;
时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列各题中,判断p是q的什么条件(请用“充分不必要条件”“必要不充分条件”“充要条件”“既不充分又不必要条件”回答):
(1)p:三角形是等腰三角形,q:三角形是等边三角形;
(2)在一元二次方程中,![]()
![]() 有实数根,
有实数根,![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①若函数![]() 的定义域为
的定义域为![]() ,则
,则![]() 一定是偶函数;
一定是偶函数;
②若![]() 是定义域
是定义域![]() 上奇函数,
上奇函数,![]() ,都有
,都有![]() ,则
,则![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
③已知![]() ,
,![]() 是函数
是函数![]() 的定义域内的任意两个值,且
的定义域内的任意两个值,且![]() ,若
,若![]() ,则
,则![]() 是定义域减函数;
是定义域减函数;
④已知是定义在![]() 上奇函数,且
上奇函数,且![]() 也为奇函数,则
也为奇函数,则![]() 是以4为周期的周期函数。
是以4为周期的周期函数。
其中真命题的有_____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)=![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com