
【题目】综合题。
(1)已知a,b∈(0,+∞),求证:x,y∈R,有 ![]() ≥
≥ ![]() ;
;
(2)若0<a<2,0<b<2,0<c<2,求证:(2﹣a)b,(2﹣b)c,(2﹣c)a不能同时大于1.
【答案】
(1)证明:( ![]() )(a+b)=x2+
)(a+b)=x2+ ![]() +y2≥x2+2xy+y2=(x+y)2,
+y2≥x2+2xy+y2=(x+y)2,
当且仅当 ![]() ,即|bx|=|ay|时取等号,
,即|bx|=|ay|时取等号,
由于a,b∈(0,+∞),所以有 ![]() ≥
≥ ![]()
(2)证明:假设结论不成立,即(2﹣a)b,(2﹣b)c,(2﹣c)a同时大于1.
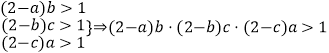 ,
,
而(2﹣a)b(2﹣b)c(2﹣c)a=(2﹣a)a(2﹣b)b(2﹣c)c
≤( ![]() )2(
)2( ![]() )2(
)2( ![]() )2=1,
)2=1,
这与(2﹣a)b(2﹣b)c(2﹣c)a>1矛盾.
所以假设错误,即(2﹣a)b,(2﹣b)c,(2﹣c)a不能同时大于1
【解析】(1)由基本不等式易得答案,注意取等条件|bx|=|ay|;(2)假设(2﹣a)b,(2﹣b)c(2﹣c)a同时大于1,推出(2﹣a)b(2﹣b)c(2﹣c)a>1 ①;再由已知条件可推出(2﹣a)b(2﹣b)c(2﹣c)a≤1,这与①矛盾,故假设不成立,即可得出结论.
【考点精析】利用反证法与放缩法对题目进行判断即可得到答案,需要熟知常见不等式的放缩方法:①舍去或加上一些项②将分子或分母放大(缩小).


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),g(x)满足:对于任意的x,都有f(﹣x)+f(x)=0,g(x)=g(|x|).当x<0时,f′(x)<0,g′(x)>0,则当x>0时,有( )
A.f'(x)>0,g′(x)>0
B.f′(x)<0,g′(x)<0
C.f′(x)<0,g′(x)>0
D.f′(x)>0,g′(x)<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
,在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形. 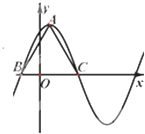
(Ⅰ)求ω的值及函数f(x)的值域;
(Ⅱ)若x∈[0,1],求函数f(x)的值域;
(Ⅲ)若 ![]() ,且
,且 ![]() ,求f(x0+1)的值.
,求f(x0+1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)= ![]() ,直线l:y=(k﹣3)x﹣k+2
,直线l:y=(k﹣3)x﹣k+2
(1)函数f(x)在x=e处的切线与直线l平行,求实数k的值
(2)若至少存在一个x0∈[1,e]使f(x0)<g(x0)成立,求实数a的取值范围
(3)设k∈Z,当x>1时f(x)的图象恒在直线l的上方,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知射线OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.
(1)当AB的中点在直线x﹣2y=0上时,求直线AB的方程;
(2)当△AOB的面积取最小值时,求直线AB的方程.
(3)当PAPB取最小值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足:在定义域D内存在实数x0 , 使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)为“1的饱和函数”.给出下列四个函数:①f(x)= ![]() ;②f(x)=2x;③f(x)=lg(x2+2);④f(x)=cos(πx).其中是“1的饱和函数”的所有函数的序号为( )
;②f(x)=2x;③f(x)=lg(x2+2);④f(x)=cos(πx).其中是“1的饱和函数”的所有函数的序号为( )
A.①③
B.②④
C.①②
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com