
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() ,过点
,过点![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,直线
两点,直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ; (Ⅱ)1
; (Ⅱ)1
【解析】
试题分析:(Ⅰ)考虑点![]() 和点
和点![]() 的关系,设点
的关系,设点![]() ,由
,由![]() 可把
可把![]() 用
用![]() 表示出来,再把
表示出来,再把![]() 代入已知抛物线方程即得; (Ⅱ)分析题意知直线
代入已知抛物线方程即得; (Ⅱ)分析题意知直线![]() 斜率存在,设
斜率存在,设![]() 方程为
方程为![]() ,设点
,设点![]() , 由直线
, 由直线![]() 方程与曲线
方程与曲线![]() 方程联立方程组,消去
方程联立方程组,消去![]() 得
得![]() 的一元二次方程,则可得
的一元二次方程,则可得![]() ,当
,当![]() 过点
过点![]() 时,不妨设
时,不妨设![]() ,则
,则![]() 可以看作是曲线
可以看作是曲线![]() 在A点处切线的斜率,则可计算出
在A点处切线的斜率,则可计算出![]() ,当
,当![]() 不过点
不过点![]() 时,计算
时,计算![]() ,最后计算
,最后计算![]() ,交把
,交把![]() 代入得到关于
代入得到关于![]() 的函数,可求得最小值.
的函数,可求得最小值.
试题解析:(Ⅰ)设点![]() ,则由
,则由![]() 得
得 ,因为点
,因为点![]() 在抛物线
在抛物线![]() 上,
上,![]()
(Ⅱ)方法一:由已知,直线![]() 的斜率一定存在,设点
的斜率一定存在,设点![]() ,设
,设![]() 方程为
方程为![]() ,
,
联立![]() 得
得![]()
由韦达定理得![]()
(1)当直线![]() 经过点
经过点![]() 即
即![]() 或
或![]() 时,当
时,当![]() 时,直线
时,直线![]() 的斜率看作抛物线在点
的斜率看作抛物线在点![]() 处的切线斜率,则
处的切线斜率,则![]() ,此时
,此时![]() ;当
;当![]() 时,同理可得
时,同理可得![]() .
.
(2)当直线![]() 不经过点
不经过点![]() 即
即![]() 且
且![]() 时,
时,![]() ,
,

![]()
![]()
![]()
所以![]() 的最小值为
的最小值为![]() .
.
方法二:同上
![]()
![]()
![]()
故![]() ,所以
,所以![]() 的最小值为
的最小值为![]()
方法三:设点![]() ,由直线
,由直线![]() 过点
过点![]() 交轨迹
交轨迹![]() 于
于![]() 两点得:
两点得:
 化简整理得:
化简整理得:
![]() ,令
,令![]() ,则
,则![]()

![]()


科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,两向量p=(2-2sin A,cos A+sin A),q=(sin A-cos A,1+sin A),且p与q是共线向量.
(1)求A的大小;
(2)求函数y=2sin2B+cos(![]() )取最大值时,角B的大小.
)取最大值时,角B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点![]() 的椭圆
的椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 为其右焦点.
为其右焦点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在平行于![]() 的直线
的直线![]() ,使得直线
,使得直线![]() 与椭圆
与椭圆![]() 有公共点,且直线
有公共点,且直线![]() 与
与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年的蔬菜销售收入均为50万元,设![]() 表示前
表示前![]() 年的纯利润总和(
年的纯利润总和(![]() =前
=前![]() 年的总收入
年的总收入![]() 前
前![]() 年的总支出
年的总支出![]() 投资额).
投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:
① 当年平均利润达到最大时,以48万元出售该厂;
② 当纯利润总和达到最大时,以16万元出售该厂,
问哪种方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)若![]() ,存在实数
,存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液.已知每投放![]() (
(![]() 且
且![]() )个单位的营养液,它在水中释放的浓度
)个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中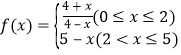 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次4个单位的营养液,则有效时间可能达几天?
(2)若先投放2个单位的营养液,3天后投放![]() 个单位的营养液.要使接下来的2天中,营养液能够持续有效,试求
个单位的营养液.要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com