
【题目】已知正方体ABCD﹣A′B′C′D′. 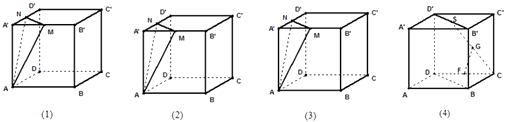
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′.
【答案】
(1)解:做出平面如图所示:
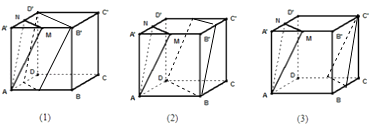
(2)解:证明:连接SD,
∵F,G分别是DC,SC的中点,
∴FG∥SD,
又SD平面BDD′B′,FD平面BDD′B′,
∴GF∥平面BDD'B'.
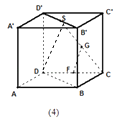
【解析】(1)在各面做△AMN的边的平行线即可得出与平面AMN平行的平面;(2)连接SD,利用中位线定理得出FG∥SD,故而GF∥平面BDD′B′.
【考点精析】根据题目的已知条件,利用棱柱的结构特征和直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列命题中正确的命题有( )个
(1)如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
(2)如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
(3)如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么
,那么![]() 平面
平面![]()
(4)如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果存在函数
,如果存在函数![]() (
(![]() 为常数),使得
为常数),使得![]() 对一切实数
对一切实数![]() 都成立,则称
都成立,则称![]() 为函数
为函数![]() 的一个承托函数,给出如下命题:
的一个承托函数,给出如下命题:
①函数![]() 是函数
是函数![]() 的一个承托函数;
的一个承托函数;
②函数![]() 是函数
是函数![]() 的一个承托函数;
的一个承托函数;
③若函数![]() 是函数
是函数![]() 的一个承托函数,则
的一个承托函数,则![]() 的取值范围是
的取值范围是![]() ;
;
④值域是![]() 的函数
的函数![]() 不存在承托函数.
不存在承托函数.
其中正确的命题的个数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,点![]() ,曲线
,曲线 ![]() ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为![]() 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.
(1)在直角坐标系中,求点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x,
cos2x,
(1)求f(x)的最小正周期及单调递减区间;
(2)当x ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sin(x﹣
=(sin(x﹣ ![]() ),sinx),函数f(x)=2
),sinx),函数f(x)=2 ![]()
![]() ,g(x)=f(
,g(x)=f( ![]() ).
).
(1)求f(x)在[ ![]() ,π]上的最值,并求出相应的x的值;
,π]上的最值,并求出相应的x的值;
(2)计算g(1)+g(2)+g(3)+…+g(2014)的值;
(3)已知t∈R,讨论g(x)在[t,t+2]上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com