
【题目】已知数列{an}满足(an+1﹣1)(an﹣1)= ![]() (an﹣an+1),a1=2,若bn=
(an﹣an+1),a1=2,若bn= ![]() .
.
(1)证明:数列{bn}是等差数列;
(2)令cn= ![]() ,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥
,{cn}的前n项和为Tn , 用数学归纳法证明Tn≥ ![]() (n∈N*).
(n∈N*).
【答案】
(1)证明:由(an+1﹣1)(an﹣1)= ![]() (an﹣an+1)得
(an﹣an+1)得 ![]() ﹣
﹣ ![]() =2,
=2,
即bn+1﹣bn=2,
∴{bn}是首项为b1= ![]() =1,公差为2的等差数列.
=1,公差为2的等差数列.
(2)解:由(1)知,bn=1+2(n﹣1)=2n﹣1,cn= ![]() =
= ![]() ,
,
①当n=1时,则有T1=1有T1≥ ![]() =1成立;
=1成立;
②假设当n=k时,不等式成立,即Tk≥ ![]() 成立,
成立,
则当n=k+1时,Tk+1=Tk+ck+1= ![]() ≥
≥ ![]() +
+ ![]() ,
,
欲证 ![]() +
+ ![]() ≥
≥ ![]() ,
,
只须证 ![]() +1≥k+1,
+1≥k+1,
即证 ![]() ≥k,即证
≥k,即证 ![]() ≥
≥ ![]() ,即证1≥0,而此式成立
,即证1≥0,而此式成立
故当n=k+1时,不等式也成立.
故有Tn≥ ![]() (n∈N*).
(n∈N*).
【解析】(1)由(an+1﹣1)(an﹣1)= ![]() (an﹣an+1)得
(an﹣an+1)得 ![]() ﹣
﹣ ![]() =2,继而得到{bn}是首项为b1=
=2,继而得到{bn}是首项为b1= ![]() =1,公差为2的等差数列.(2)由数学归纳法和分析法即可证明.
=1,公差为2的等差数列.(2)由数学归纳法和分析法即可证明.
【考点精析】利用等差关系的确定和数学归纳法的定义对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数学归纳法是证明关于正整数n的命题的一种方法.
)那么这个数列就叫做等差数列;数学归纳法是证明关于正整数n的命题的一种方法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),函数f(x)=
=(sinx,sinx),函数f(x)= ![]() .
.
(1)求f(x)的对称轴方程;
(2)求使f(x)≥1成立的x的取值集合;
(3)若对任意实数 ![]() ,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
,不等式f(x)﹣m<2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求b的值;
(Ⅱ)判断函数f(x)的单调性;
(Ⅲ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)同时满足①对于定义域上的任意x,恒有f(x)+f(﹣x)=0;②对于定义域上的任意x1、x2 , 当x1≠x2时,恒有 ![]() <0,则称函数f(x)为“理想函数”.给出下列三个函数中:(1)f(x)=
<0,则称函数f(x)为“理想函数”.给出下列三个函数中:(1)f(x)= ![]() ;(2)f(x)=x+1;(3)f(x)=
;(2)f(x)=x+1;(3)f(x)= ![]() ,能被称为“理想函数”的有(填相应的序号).
,能被称为“理想函数”的有(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
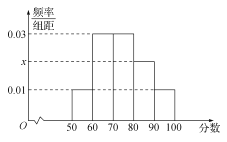
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数中,表示同一函数的是( )
A.y=1,y= ![]()
B.y= ![]() ×
× ![]() ,y=
,y= ![]()
C.y=2x+1﹣2x , y=2x
D.y=2lgx,y=lgx2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com