
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD= ![]() BC=2,E在BC上,且BE=
BC=2,E在BC上,且BE= ![]() AB=1,侧棱PA⊥平面ABCD.
AB=1,侧棱PA⊥平面ABCD. 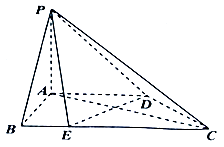
(1)求证:平面PDE⊥平面PAC;
(2)若△PAB为等腰直角三角形. (i)求直线PE与平面PAC所成角的正弦值;
(ii)求二面角A﹣PC﹣D的余弦值.
【答案】
(1)证明:∵PA⊥平面ABCD,∴AB⊥PA,
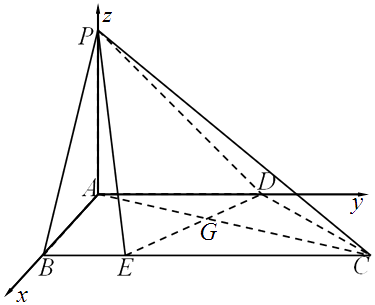
又∵AB⊥AD,故可建立建立如图所示坐标系.
由已知D(0,2,0),E(2,1,0),C(2,4,0),P(0,0,λ),(λ>0)
∴ ![]() =(2,4,0),
=(2,4,0), ![]() =(0,0,λ),
=(0,0,λ), ![]() =(2,﹣1,0),
=(2,﹣1,0),
∴ ![]() =4﹣4+0=0,
=4﹣4+0=0, ![]() .,
.,
∴DE⊥AC,DE⊥AP,∴ED⊥平面PAC,
∵ED平面PDE,平面PDE⊥平面PAC
(2)解:(i)由(1)得,平面PAC的一个法向量是 ![]() =(2,﹣1,0),
=(2,﹣1,0),
∵△PAB为等腰直角三角形,故PA=2, ![]() .
.
设直线PE与平面PAC所成的角为θ,
则 ![]() =
= 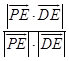 =
= ![]() =
= ![]() ,
,
∴直线PE与平面PAC所成角的正弦值为 ![]() .
.
(ii)设平面PCD的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
![]() =(2,2,0),
=(2,2,0), ![]() =(0,﹣2,2),
=(0,﹣2,2),
则 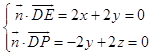 ,令x=1,则
,令x=1,则 ![]() =(1,﹣1,﹣1),
=(1,﹣1,﹣1),
∴cos< ![]() >=
>= 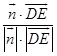 =
= ![]() .
.
∵二面角A﹣PC﹣D的平面角是锐角,
∴二面角A﹣PC﹣D的余弦值为 ![]() .
.
【解析】(1)由AB⊥PA,AB⊥AD,建立建立空间直角坐标系,利用向量法能证明平面PDE⊥平面PAC.(2)(i)求出平面PAC的一个法向量和 ![]() ,利用向量法能求出直线PE与平面PAC所成角的正弦值.(ii)求出平面PCD的一个法向量,利用向量法能求出二面角A﹣PC﹣D的余弦值.
,利用向量法能求出直线PE与平面PAC所成角的正弦值.(ii)求出平面PCD的一个法向量,利用向量法能求出二面角A﹣PC﹣D的余弦值.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直),还要掌握空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】设 ![]() (a,b为实常数).
(a,b为实常数).
(1)当a=b=1时,证明:f(x)不是奇函数;
(2)设f(x)是奇函数,求a与b的值;
(3)当f(x)是奇函数时,研究是否存在这样的实数集的子集D,对任何属于D的x、c,都有f(x)<c2﹣3c+3成立?若存在试找出所有这样的D;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上.
=1(a>b>0)的左焦点为F1(﹣1,0),离心率是e,点(1,e)在椭圆上. 
(1)求椭圆C的方程;
(2)设点M(2,0),过点F1的直线交C于A,B两点,直线MA,MB与直线x=﹣2分别交于P,Q两点,求△MPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数y=f(x)满足:函数y=f(x+1)的图象关于直线x=﹣1对称,且当x∈(﹣∞,0)时,f(x)+xf′(x)<0成立(f′(x)是函数f(x)的导函数),若a=0.76f(0.76),b=log ![]() 6f(log
6f(log ![]() 6),c=60.6f(60.6),则a,b,c的大小关系是( )
6),c=60.6f(60.6),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a、b∈M,
(1)证明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移
sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移 ![]() 个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是( )
个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六面体ABCD﹣A1B1C1D1中,M,N分别是棱A1B1 , B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1 . 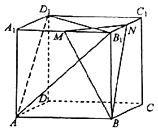
(1)证明:BB1⊥平面ABCD;
(2)已知六面体ABCD﹣A1B1C1D1的棱长均为 ![]() ,cos∠BAD=
,cos∠BAD= ![]() ,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
,设平面BMN与平面AB1D1相交所成二面角的大小为θ求cosθ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l与平面α相交但不垂直,m为空间内一条直线,则下列结论一定不成立的是( )
A.m⊥l,mα
B.m⊥l,m∥α
C.m∥l,m∩α≠
D.m⊥l,m⊥α
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com