
����Ŀ�����������ʱ����ijЬ������һ����Ϊ50![]() ����
����![]() ����ƽ�澵����һ����ֱ�ڷŵļ���Ь�������ݾ��飺һ��˿�
����ƽ�澵����һ����ֱ�ڷŵļ���Ь�������ݾ��飺һ��˿�![]() ���۾�
���۾�![]() ������ľ���Ϊ
������ľ���Ϊ![]() ��
��![]() ��������
��������![]() �ڣ���֧��
�ڣ���֧��![]() ��Ϊ
��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ���˿Ϳ��ӵľ���ΧΪ
���˿Ϳ��ӵľ���ΧΪ![]() ����ͼ��ʾ������
����ͼ��ʾ������![]() �ij���Ϊ
�ij���Ϊ![]() ��
��![]() ��.
��.
��I����![]() ʱ������
ʱ������![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��![]() �����ֵ��
�����ֵ��
��II�����˿͵�Ь![]() �ھ��е���
�ھ��е���![]() ���㲻�ȹ�ϵ
���㲻�ȹ�ϵ![]() ������Ь����ʱ���ƹ˿Ϳ��ھ��п����Լ���Ь����ʹһ��˿Ͷ����ھ��п����Լ���Ь������
������Ь����ʱ���ƹ˿Ϳ��ھ��п����Լ���Ь����ʹһ��˿Ͷ����ھ��п����Լ���Ь������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
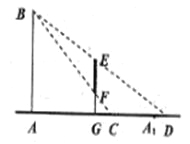
���𰸡���I������������II��![]() .
.
��������
��I�����������ε����ƣ����![]() ��
��![]() �ij����Ӷ��ɹ���������������ȷ�������ĵ����ԣ�������ý��ۣ���II�����������ε����ƣ����
�ij����Ӷ��ɹ���������������ȷ�������ĵ����ԣ�������ý��ۣ���II�����������ε����ƣ����![]() ��
��![]() ��������֪
��������֪![]() ����
����![]() ��
��![]() ��������Ӷ�
��������Ӷ� ��
��![]() ��������ɴ˿����
��������ɴ˿����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��I����Ϊ![]() ��
��![]() ��������
��������![]() ����
����![]() �����
�����![]() ��ͬ������
��ͬ������![]() ����
����![]() �����
�����![]() ������
������![]() ��
��![]() ��Ϊ
��Ϊ![]() ������
������![]() ��
��![]() �ϵ����ݼ����ʵ�
�ϵ����ݼ����ʵ�![]() ʱ��
ʱ��![]() ȡ�����ֵΪ
ȡ�����ֵΪ![]()
��II����![]() ����
����![]() ����
����![]() ����
����![]() ������������֪
������������֪![]() ����
����![]() ��
��![]() ��������Ӷ�
��������Ӷ� ��
��![]() ����������
���������� ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
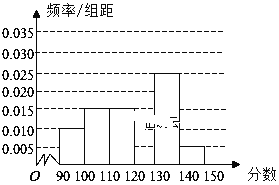
����Ŀ��ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ![]() ��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����
��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����![]() ��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
��1���������![]() �ڵ�Ƶ�ʣ���ȫ���Ƶ�ʷֲ�ֱ��ͼ�����ݴ˹��Ʊ��ο��Ե�ƽ���֣�
�ڵ�Ƶ�ʣ���ȫ���Ƶ�ʷֲ�ֱ��ͼ�����ݴ˹��Ʊ��ο��Ե�ƽ���֣�
��2���÷ֲ�����ķ������ڷ�����Ϊ![]() ��ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2������������1���ڷ�����
��ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2������������1���ڷ�����![]() �ڵĸ���
�ڵĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
��1����![]() ʱ����
ʱ����![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ʱ����������
ʱ����������![]() ������
������![]() ��������
��������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ��������꼶ѧ�����������������������ķ�����ȡ80��ѧ�����õ��������������Ƶ�ʷֲ�ֱ��ͼ��ͼ1����Ů�����������Ƶ�ʷֲ�ֱ��ͼ��ͼ2��.��֪ͼ1��������170��175cm������������16��
.

(1)����Ƶ�ʷֲ�ֱ��ͼ��������е�![]() �����������ж����ж�ٷֱȣ��İ�����Ϊ���������Ա��йء���
�����������ж����ж�ٷֱȣ��İ�����Ϊ���������Ա��йء���
|
| �ܼ� | |
�������� | |||
������ | |||
�ܼ� |
(2)������80��ѧ���У���������170-175cm֮���ѧ�����С�Ů�Ա�ֲ�����ķ��������5�ˣ�����5����ѡ��3�˵����֣���3����ǡ����һ��Ů���ĸ���.
| 0.025 | 0.610 | 0.005 | 0.001 |
| 5.024 | 4.635 | 7.879 | 10.828 |
�ο���ʽ���ο��������£�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ú졢�ơ������ֲ�ͬ��ɫ��ͼ�е�![]() ���������Ϳɫ��ÿ������ֻͿһ����ɫ����
���������Ϳɫ��ÿ������ֻͿһ����ɫ����![]() ��������ɫ����ͬ�ĸ�����________��
��������ɫ����ͬ�ĸ�����________��![]() ��������ɫ����ͬ�ĸ�����________.
��������ɫ����ͬ�ĸ�����________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������5����С�ʵ���ȫ��ͬ��������2������3�������в��Żص������������2�����������¼��ĸ��ʣ�
��1��A=����һ����������
��2��B=���ڶ�����������
��3��AB=�������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˵���Ƥ�е���Ƥ��˫��Ƥ֮�֣������ɶ�Ӧ�Ļ��������.����ѧ���Ѿ�֤����������Ƥ��˫�Ļ��������֣�һ�������Ի���Ϊ![]() ������һ�������Ի���Ϊ
������һ�������Ի���Ϊ![]() �����������dzɶԳ��֣���
�����������dzɶԳ��֣���![]() ��
��![]() ��
��![]() ��
��![]() �������ɶԵĻ����У�ֻҪ���������Ի�����ô����˾�һ����˫��Ƥ��Ҳ����˵��������Ƥ���ij�Ҫ�����ǡ��ɶԵĻ�����
�������ɶԵĻ����У�ֻҪ���������Ի�����ô����˾�һ����˫��Ƥ��Ҳ����˵��������Ƥ���ij�Ҫ�����ǡ��ɶԵĻ�����![]() �������������������ͻ��Ļ����ɶԵĻ����У�һ�����Ը��ף���һ������ĸ�ף�����ĸ���ṩ����ʱ���������.��һ�Է��ޣ����˳ɶԵĻ�����
�������������������ͻ��Ļ����ɶԵĻ����У�һ�����Ը��ף���һ������ĸ�ף�����ĸ���ṩ����ʱ���������.��һ�Է��ޣ����˳ɶԵĻ�����![]() �������ǻ���ͻ�䣬�����ǵĺ����ǵ���Ƥ�ĸ���.
�������ǻ���ͻ�䣬�����ǵĺ����ǵ���Ƥ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C�Ķ���ΪO��0��0��������F��0��1��
��������������C�ķ��̣�
��������F��ֱ�߽���������A��B���㣮��ֱ��OA��OB�ֱ�ֱ��l��y=x��2��M��N���㣬��|MN|����Сֵ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com