
已知函数 ,
,
 .
.
(Ⅰ)若 ,求函数
,求函数 在区间
在区间 上的最值;
上的最值;
(Ⅱ)若 恒成立,求
恒成立,求 的取值范围.
的取值范围.
注: 是自然对数的底数
是自然对数的底数
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)将 代入函数解析式,并将函数
代入函数解析式,并将函数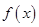 解析式中的绝对值去掉,写成分段函数,并将定义域
解析式中的绝对值去掉,写成分段函数,并将定义域 分为两部分:
分为两部分: 与
与 ,利用导数分别求出函数
,利用导数分别求出函数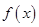 在区间
在区间 与
与 上的最大值与最小值,然后进行比较,最终确定函数
上的最大值与最小值,然后进行比较,最终确定函数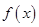 在区间
在区间 上的最大值与最小值;(Ⅱ)利用参数分离法将不等式进行转化,借助“大于最大值,小于最小值”的思想求参数
上的最大值与最小值;(Ⅱ)利用参数分离法将不等式进行转化,借助“大于最大值,小于最小值”的思想求参数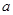 的取值范围,不过在去绝对值符号的时候要对自变量
的取值范围,不过在去绝对值符号的时候要对自变量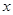 的范围进行取舍(主要是自变量
的范围进行取舍(主要是自变量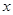 的范围决定
的范围决定 的符号).
的符号).
试题解析:(Ⅰ) 若 ,则
,则 .
.
当 时,
时, ,
, ,
,
所以函数 在
在 上单调递增;
上单调递增;
当 时,
时, ,
, .
.
所以函数 在区间
在区间 上单调递减,
上单调递减,
所以 在区间
在区间 上有最小值
上有最小值 ,又因为
,又因为 ,
, ,而
,而 ,
,
所以 在区间
在区间 上有最大值
上有最大值 .
.
(Ⅱ)函数 的定义域为
的定义域为 .
.
由 ,得
,得 . (*)
. (*)
(ⅰ)当 时,
时, ,
, ,
,
不等式(*)恒成立,所以
 ;
;
(ⅱ)当 时,
时,
①当 时,由
时,由 得
得 ,即
,即 ,
,
现令 , 则
, 则 ,
,
因为 ,所以
,所以 ,故
,故 在
在 上单调递增,
上单调递增,
从而 的最小值为
的最小值为 ,因为
,因为 恒成立等价于
恒成立等价于 ,
,
所以 ;
;
②当 时,
时, 的最小值为
的最小值为 ,而
,而 ,显然不满足题意.
,显然不满足题意.
综上可得,满足条件的 的取值范围是
的取值范围是 .
.
考点:利用导数求函数的最值、分段函数、参数分离法


科目:高中数学 来源: 题型:解答题
(本小题13分)已知函数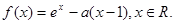
(1)若实数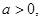 求函数
求函数 在
在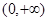 上的极值;
上的极值;
(2)记函数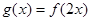 ,设函数
,设函数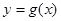 的图像
的图像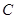 与
与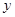 轴交于
轴交于 点,曲线
点,曲线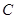 在
在 点处的切线与两坐标轴所围成图形的面积为
点处的切线与两坐标轴所围成图形的面积为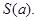 则当
则当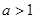 时,求
时,求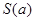 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数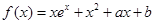 在点
在点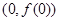 处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+
处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+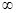 )均有
)均有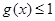 恒成立.
恒成立.
(Ⅰ)求a,b,c的值;
(Ⅱ)求证: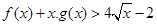 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数F(x )=x2+aln(x+1)
(I)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a的取值范围;
(II)若函数y=f(x)有两个极值点x1,x2且 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数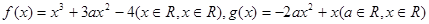 (Ⅰ)若函数
(Ⅰ)若函数 在
在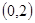 上单调递减,在区间
上单调递减,在区间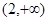 单调递增,求
单调递增,求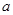 的值;
的值;
(Ⅱ)若函数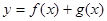 在
在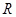 上有两个不同的极值点,求
上有两个不同的极值点,求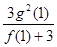 的取值范围;
的取值范围;
(Ⅲ)若方程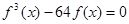 有且只有三个不同的实根,求
有且只有三个不同的实根,求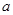 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com