
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】有人收集了七月份的日平均气温![]() (摄氏度)与某次冷饮店日销售额
(摄氏度)与某次冷饮店日销售额![]() (百元)的有关数据,为分析其关系,该店做了五次统计,所得数据如下:
(百元)的有关数据,为分析其关系,该店做了五次统计,所得数据如下:
日平均气温 | 31 | 32 | 33 | 34 | 35 |
日销售额 | 5 | 6 | 7 | 8 | 10 |
由资料可知,![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,给出下列说法:
,给出下列说法:
①![]() ;
;
②日销售额![]() (百元)与日平均气温
(百元)与日平均气温![]() (摄氏度)成正相关;
(摄氏度)成正相关;
③当日平均气温为![]() 摄氏度时,日销售额一定为
摄氏度时,日销售额一定为![]() 百元.
百元.
其中正确说法的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在改革开放40年成就展上某地区某农产品近几年的产量统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)根据线性回归方程预测2020年该地区该农产品的年产量.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为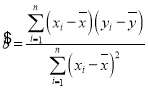 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留到小数点后两位)
,计算结果保留到小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县精准扶贫攻坚力公室决定派遣8名干部(5男3女)分成两个小组,到该县甲、乙两个贫困村去参加扶贫工作,若要求每组至少3人,且每组均有男干部参加,则不同的派遣方案共有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“互倒函数”的定义如下:对于定义域内每一个![]() ,都有
,都有![]() 成立,若现在已知函数
成立,若现在已知函数![]() 是定义域在
是定义域在![]() 的“互倒函数”,且当
的“互倒函数”,且当![]() 时,
时,![]() 成立.若函数
成立.若函数![]() (
(![]() )都恰有两个不同的零点,则实数
)都恰有两个不同的零点,则实数![]() 的取值范围是( )
的取值范围是( )
A.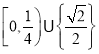 B.
B.![]() C.
C.![]() D.
D.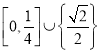
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com