Question

【题目】袋中有大小相同的红、黄两种颜色的球各1个，从中任取1只，有放回地抽取3次． 求：
（1）3只全是红球的概率；
（2）3只颜色全相同的概率；
（3）3只颜色不全相同的概率．

Answer 1

【答案】
（1）解：由题意知本题是一个相互独立事件同时发生的概率，

从袋中摸球，摸到红球的概率是 ，

三次有放回到摸球可以看做是三次独立重复试验，

∴P=

（2）解：利用树状图我们可以列出有放回地抽取3次球的所有可能结果：

， ．

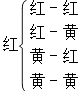3只颜色全相同的概率为P2=2× =2 = ．

（3）解：3只颜色不全相同的概率为 （或 ）
【解析】（1）由题意知本题是一个相互独立事件同时发生的概率，从袋中摸球，摸到红球的概率是 ，三次有放回到摸球可以看做是三次独立重复试验，根据概率公式得到结果．（2）三只颜色全相同，则可能抽到红色和黄色两种情况，这两种情况是互斥的，根据做出的每个球被抽到的概率和相互独立事件同时发生的概率和互斥事件的概率，得到结果．（3）根据二问做出的结果，三只颜色不全相同，是三只颜色全部相同的对立事件，用对立事件的概率得到结果，或者是用树状图列出的结果求出比值．
【考点精析】认真审题，首先需要了解互斥事件与对立事件(互斥事件是指事件A与事件B在一次试验中不会同时发生，其具体包括三种不同的情形：（1）事件A发生且事件B不发生；（2）事件A不发生且事件B发生；（3）事件A与事件B同时不发生；而对立事件是指事件A与事件B有且仅有一个发生，其包括两种情形；（1）事件A发生B不发生；（2）事件B发生事件A不发生，对立事件互斥事件的特殊情形)．