
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点P
,点P![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)设![]() 分别为椭圆C的左右焦点,过
分别为椭圆C的左右焦点,过![]() 的直线
的直线![]() 与椭圆C交于不同的两点A、B,求△
与椭圆C交于不同的两点A、B,求△![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥VABCD中,底面ABCD是矩形,VD⊥平面ABCD,过AD的平面分别与VB,VC交于点M,N.

(1) 求证:BC⊥平面VCD;
(2) 求证:AD∥MN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个函数![]() ,其中
,其中![]() ,
,![]() 的图像如图所示.
的图像如图所示.

(1)请在坐标系中画出![]() ,
,![]() 的图像,并根据这四个函数的图像总结出指数函数具有哪些性质?
的图像,并根据这四个函数的图像总结出指数函数具有哪些性质?
(2)举出在实际情境中能够抽象出指数函数的一个例子并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作之一,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积![]() (弦
(弦![]() 矢
矢![]() 矢
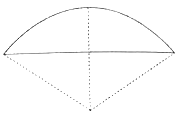
矢![]() ),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
A.12平方米B.16平方米C.20平方米D.24平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
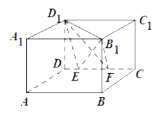
【题目】如图,设![]() ,
,![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,
,![]() ,其中正确的命题为( )
,其中正确的命题为( )
A.三棱锥![]() 的体积为定值
的体积为定值
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.![]() 平面
平面![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com