练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．如图，长方体ABCD-A1B1C1D1中，AB=AD，点P为DD1的中点．
    （1）求证：直线BD1∥平面PAC；
    （2）求证：平面PAC⊥平面BDD1．

    分析 （1）设AC和BD交于点O，连PO，则PO∥BD1，由此能证明直线BD1∥平面PAC．
    （2）推导出AC⊥BD，DD1⊥AC，由此能证明平面PAC⊥平面BDD1．

    解答 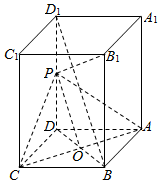证明：（1）设AC和BD交于点O，连PO，
    由P，O分别是DD1，BD的中点，故PO∥BD1，
    因为PO?平面PAC，BD1?平面PAC，
    所以直线BD1∥平面PAC
    （2）长方体ABCD-A1B1C1D1中，AB=AD=1，
    底面ABCD是正方形，则AC⊥BD
    又DD1⊥面ABCD，则DD1⊥AC，
    所以AC⊥面BDD1，则平面PAC⊥平面BDD1．

    点评 本题主要考查了线面平行和线面垂直的判定定理的应用．考查了学生对基本定理的记忆和灵活运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．两人打靶，甲击中目标的概率为0.8，乙击中目标的概率为0.7，若两人同时射击一目标，则他们都击中目标的概率是（　　）
    A．0.6B．0.48C．0.75D．0.56

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．将直线l向左平移$\sqrt{3}$个单位，再向上平移1个单位后所得直线与l重合，则直线l的倾斜角为（　　）
    A．30°B．60°C．120°D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在直角△ABC 中，∠A=90°，M 是BC 的中点，$\overrightarrow{AB}$=3$\overrightarrow{AN}$，$\overrightarrow{BM}$•$\overrightarrow{CN}$=-$\frac{5}{13}$$\overrightarrow{BC}$2，则tan∠ABC=（　　）
    A．$\frac{1}{2}$B．2C．$\frac{3}{2}$D．$\frac{\sqrt{17}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-4，7），$\overrightarrow{a}$+$\overrightarrow{c}$=0，则$\overrightarrow{c}$在$\overrightarrow{b}$方向上的投影为$-\frac{\sqrt{65}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知△ABC，若存在△A1B1C1，满足$\frac{cosA}{{sin{A_1}}}=\frac{cosB}{{sin{B_1}}}=\frac{cosC}{{sin{C_1}}}=1$，则称△A1B1C1是△ABC的一个“友好”三角形．在满足下述条件的三角形中，存在“友好”三角形的是②：（请写出符合要求的条件的序号）
    ①A=90°，B=60°，C=30°；②A=75°，B=60°，C=45°； ③A=75°，B=75°，C=30°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=sin2x+sin2（x+α）+sin2（x+β），其中α，β是适合0≤α≤β≤π的常数
    （1）若$α=\frac{π}{4}，β=\frac{3π}{4}$，求函数f（x）的最小值；
    （2）f（x）是否可能为常值函数？若可能，求出f（x）为常值函数时，α，β的值，如果不可能，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．在下列结论中，正确结论的序号为①②④．
    ①函数y=sin（kπ-x）（k∈Z）为奇函数；
    ②若tan（π-x）=2，则${cos^2}x=\frac{1}{5}$；
    ③函数$y=tan（{2x+\frac{π}{6}}）$的图象关于点$（{\frac{π}{12}，0}）$对称；
    ④函数$y=cos（{2x+\frac{π}{3}}）$的图象的一条对称轴为$x=-\frac{2π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．下面使用类比推理正确的是（　　）
    A．直线a，b，c，若a∥b，b∥c，则a∥c．类推出：向量$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$，若$\overrightarrow a$∥$\overrightarrow b$，$\overrightarrow b$∥$\overrightarrow c$，则$\overrightarrow a$∥$\overrightarrow c$
    B．同一平面内，直线a，b，c，若a⊥c，b⊥c，则a∥b．类推出：空间中，直线a，b，c，若a⊥c，b⊥c，则a∥b
    C．若a，b∈R，则a-b＞0⇒a＞b．类推出：若a，b∈C，则a-b＞0⇒a＞b
    D．由向量加法的几何意义，可以类比得到复数加法的几何意义．

    查看答案和解析>>

    同步练习册答案