
 ;
; ,进而可得a:|f(1)|+2|f(2)|+|f(3)|<2,,再分析,|f(1)|+2|f(2)|+|f(3)|三项的和,可得矛盾,即可证原命题成立.
,进而可得a:|f(1)|+2|f(2)|+|f(3)|<2,,再分析,|f(1)|+2|f(2)|+|f(3)|三项的和,可得矛盾,即可证原命题成立. ,则有:|f(1)|+2|f(2)|+|f(3)|<
,则有:|f(1)|+2|f(2)|+|f(3)|< +2×
+2× +
+ =2,
=2,

科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市潜山中学高三(上)第三次月考数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省镇江市大港中学高三(上)数学综合练习(二)(解析版) 题型:解答题
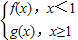 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com