
【题目】设![]() 为抛物线
为抛物线![]() 的准线上一点,F为C 的焦点,点P在C上且满足
的准线上一点,F为C 的焦点,点P在C上且满足![]() ,若当m取得最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则该双曲线的离心率为
,若当m取得最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则该双曲线的离心率为
A. ![]() B. 3 C.
B. 3 C. ![]() D.
D. ![]()
【答案】B
【解析】分析:由题意首先确定抛物线的方程,然后结合几何关系将原问题转化为直线与抛物线相切的问题,最后求解双曲线的离心率即可.
详解:![]() 为抛物线
为抛物线![]() 的准线上一点,
的准线上一点,
则![]() ,解得p=6;
,解得p=6;
∴抛物线的标准方程为y2=12x,焦点为F(3,0),准线方程为x=3;
过点P作准线的垂线,垂足为N,则由抛物线的定义可得|PN|=|PF|,
∵|PF|=m|PA|,∴|PN|=m|PA|,∴![]() ;
;
如图所示,
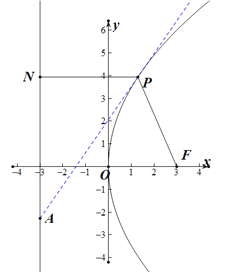
设PA的倾斜角为![]() ,则
,则![]() ,
,
当m取得最小值时,![]() 最小,此时直线PA与抛物线相切;
最小,此时直线PA与抛物线相切;
设直线PA的方程为![]() ,代入y2=12x,
,代入y2=12x,
可得![]() .
.
∴![]() ,
,
解得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
可得切点![]() ;
;
由题意可得双曲线的焦点为(3,0),(3,0),
∴双曲线的实轴长为![]() .
.
∴双曲线的离心率为![]() .
.
本题选择B选项.


科目:高中数学 来源: 题型:
【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0,![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知(x)=![]() ,x∈[0,1]利用上述性质,求函数f(x)的值域;
,x∈[0,1]利用上述性质,求函数f(x)的值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x+2a.若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方形ABCD,AD=2CD=4,M、N分别为AD、BC的中点,将长方形ABCD沿MN折到MNFE位置,且使平面MNFE⊥平面ABCD.
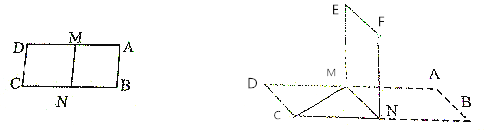
(1)求证:直线CM⊥面DFN;
(2)求点C到平面FDM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在[0,π]上的图象.
在[0,π]上的图象.

(2)若![]() 偶函数,求
偶函数,求![]()
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标变为原来的4倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期著名的数学家秦九韶在其著作《数书九章》中,提出了已知三角形三边长求三角形的面积的公式,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即 ,其中a、b、c分别为
,其中a、b、c分别为![]() 内角A、B、C的对边.若
内角A、B、C的对边.若![]() ,
,![]() ,则
,则![]() 面积S的最大值为
面积S的最大值为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线2x+y-5=0与x-2y=0的交点P.
(1)若直线l平行于直线l1:4x-y+1=0,求l的方程;
(2)若直线l垂直于直线l1:4x-y+1=0,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业2017年的纯利润为500万元,因设备老化等原因,企业的生产能力逐年下降,若不能进行技术改造,预测从2018年起每年比上一年纯利润减少20万元,2018年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第![]() 年(以2018年为第一年)的利润为
年(以2018年为第一年)的利润为![]() 万元(
万元(![]() 为正整数).
为正整数).
(1)设从今年起的前![]() 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,从2018年起该企业至少经过多少年,进行技术改造后的累计利润超过不进行技术改造的累计纯利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com