
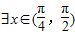 ,使mcosx=2sinx成立;命题q:函数
,使mcosx=2sinx成立;命题q:函数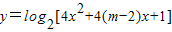 的定义域为(-∞,+∞),若“p∨q”为真,“p∧q”为假,求m的取值范围.
的定义域为(-∞,+∞),若“p∨q”为真,“p∧q”为假,求m的取值范围.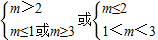 ,由此解得m的取值范围.
,由此解得m的取值范围.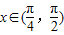 时,y=2tanx为增函数,
时,y=2tanx为增函数,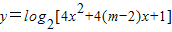 的定义域为(-∞,+∞),
的定义域为(-∞,+∞),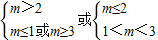 ,解得m≥3,或1<m≤2.
,解得m≥3,或1<m≤2.

科目:高中数学 来源:2010-2011学年浙江省高三上学期11月月考理科数学卷 题型:选择题
已知命题p: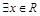 ,使
,使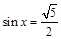 ;命题q:
;命题q: ,都有
,都有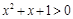 .给出下列结论:
.给出下列结论:
①命题“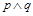 ”是真命题 ②命题“
”是真命题 ②命题“ ”是真命题
”是真命题
③命题“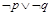 ”是假命题 ④命题“
”是假命题 ④命题“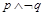 ”是假命题
”是假命题
其中正确的是
(A)②③ (B)②④ (C)③④ (D)①②③
查看答案和解析>>
科目:高中数学 来源:2010年湖北省秋季高二期末考试数学理卷 题型:填空题
.已知命题p: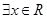 ,使
,使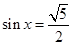 ;命题q:
;命题q: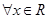 ,都有
,都有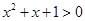 ,给出下列结论:①命题“p∧q”是真命题;②命题“p∧
,给出下列结论:①命题“p∧q”是真命题;②命题“p∧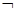 q”是假命题;③命题“p∨q”是真命题;④命题“
q”是假命题;③命题“p∨q”是真命题;④命题“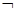 p∨
p∨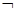 q”是假命题,其中正确的是_____________.(填写正确的序号)
q”是假命题,其中正确的是_____________.(填写正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:![]() ,使
,使![]() ;命题q:
;命题q:![]() ,都有
,都有![]() ,给出下列结论:①命题“p∧q”是真命题;②命题“p∧
,给出下列结论:①命题“p∧q”是真命题;②命题“p∧![]() q”是假命题;③命题“p∨q”是真命题;④命题“
q”是假命题;③命题“p∨q”是真命题;④命题“![]() p∨
p∨![]() q”是假命题,其中正确的是_____________.(填写正确的序号)
q”是假命题,其中正确的是_____________.(填写正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com