
下列四个命题
p1:?x∈(0,+∞),( )x<(
)x<( )x;
)x;
p2:?x∈(0,1),lo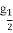 x>lo
x>lo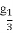 x;
x;
p3:?x∈(0, +∞),( )x>lo
)x>lo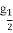 x;
x;
p4:?x∈(0, ),(
),( )x<lo
)x<lo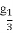 x.
x.
其中的真命题是( )
(A)p1,p3 (B)p1,p4 (C)p2,p3 (D)p2,p4
D
【解析】【思路点拨】根据含有全称量词的命题为真的情况使用指数函数、对数函数的性质进行判断.含有全称量词的命题为假的情况只要找出反例,对特称命题为真的判断,只要找出一个值使命题为真,含有存在量词的命题为假的判断结合函数性质进行.
解:根据指数函数的性质,对 x∈(0,+∞),(
x∈(0,+∞),( )x>(
)x>( )x,故命题p1是假命题;由于lo
)x,故命题p1是假命题;由于lo x-lo
x-lo x=
x= -
-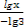 =
=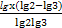 ,故对
,故对 x∈(0,1),lo
x∈(0,1),lo x>lo
x>lo x,故
x,故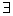 x∈(0,1),lo
x∈(0,1),lo x>lo
x>lo x,命题p2是真命题;当x∈(0,
x,命题p2是真命题;当x∈(0, )时,(
)时,( )x<1,lo
)x<1,lo x>1,故(
x>1,故( )x>lo
)x>lo x不成立,命题p3是假命题;
x不成立,命题p3是假命题;  x∈(0,
x∈(0, ),(
),( )x<1,lo
)x<1,lo x>1,故(
x>1,故( )x<lo
)x<lo x恒成立,命题p4是真命题.故选D.
x恒成立,命题p4是真命题.故选D.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(八)第二章第五节练习卷(解析版) 题型:解答题
已知函数f(x)=-x+log2 .
.
(1)求f( )+f(-
)+f(- )的值.
)的值.
(2)当x∈(-a,a],其中a∈(0,1),a是常数时,函数f(x)是否存在最小值?若存在,求出f(x)的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(二)第一章第二节练习卷(解析版) 题型:选择题
下列各小题中,p是q的充要条件的是( )
(1)p:m<-2或m>6;q:y=x2+mx+m+3有两个不同的零点.
(2)p: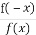 =1;q:y=f(x)是偶函数.
=1;q:y=f(x)是偶函数.
(3)p:cosα=cosβ;q:tanα=tanβ.
(4)p:A∩B=A;q: 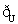 B⊆
B⊆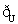 A.
A.
(A)(1)(2) (B)(2)(3)
(C)(3)(4) (D)(1)(4)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(九)第二章第六节练习卷(解析版) 题型:选择题
实数a=0. ,b=log30.3,c=
,b=log30.3,c= 的大小关系正确的是( )
的大小关系正确的是( )
(A)a<c<b (B)a<b<c
(C)b<a<c (D)b<c<a
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:填空题
已知条件p:x2-x≥6;q:x∈Z,当x∈M时,“p且q”与“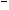 q”同时为假命题,则x取值组成的集合M= .
q”同时为假命题,则x取值组成的集合M= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(三)第一章第三节练习卷(解析版) 题型:选择题
命题“?x∈[1,2],x2-a≤0”为真命题的一个充分而不必要条件是( )
(A)a≥4 (B)a≤4 (C)a≥5 (D)a≤5
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
设l,m,n为三条不同的直线,α,β为两个不同的平面,下列命题中正确的个数是( )
①若l⊥α,m∥β,α⊥β,则l⊥m;
②若m?α,n?α,l⊥m,l⊥n,则l⊥α;
③若l∥m,m∥n,l⊥α,则n⊥α;
④若l∥m,m⊥α,n⊥β,α∥β,则l∥n.
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com