Question

14．已知圆C：x²+y²+Dx+Ey+9=0关于直线4x+y=0对称，且半径为2$\sqrt{2}$，圆心在第四象限．
（Ⅰ）求圆C的方程；
（Ⅱ）点M在圆C内部，且满足：$\left\{\begin{array}{l}{x≥2}\\{x-y-5≥0}\\{x+y+3≥0}\end{array}\right.$，求2x-y的取值范围．

Answer 1

分析 （1）由已知可得圆心（-$\frac{D}{2}$，-$\frac{E}{2}$）在直线4x+y=0上，结合圆半径为2$\sqrt{2}$，圆心在第四象限，可得答案；
（2）画出满足条件的可行域，数形结合求出2x-y的最值，可得2x-y的取值范围．

解答 解：（I）∵圆C：x²+y²+Dx+Ey+9=0关于直线4x+y=0对称，
∴圆心（-$\frac{D}{2}$，-$\frac{E}{2}$）在直线4x+y=0上，
又∵半径为2$\sqrt{2}$，圆心在第四象限，
∴$\left\{\begin{array}{l}-2D-\frac{E}{2}=0\\ \frac{\sqrt{{D}^{2}+{E}^{2}-36}}{2}=2\sqrt{2}\\-\frac{D}{2}＞0\\-\frac{E}{2}＜0\end{array}\right.$，
解得：$\left\{\begin{array}{l}D=-2\\ E=8\end{array}\right.$，
∴圆C的方程为：x²+y²-2x+8y+9=0；
（Ⅱ）点M在圆C内部，且满足：$\left\{\begin{array}{l}x≥2\\ x-y-5≥0\\ x+y+3≥0\end{array}\right.$，
故M对应的平面区域如下图所示：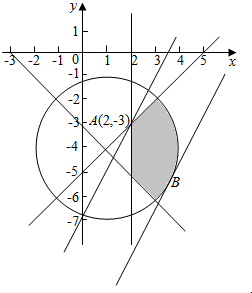

由图可得：当直线y=2x-z过A（2，-3）时，Z=2x-y取最大值7，
当当直线y=2x-z与圆切于B点时，Z=2x-y取最小值，
由此时圆心（1，-4）到直线y=2x-z的距离d=$\frac{|6-z|}{\sqrt{5}}$=2$\sqrt{2}$得：
z=6-$2\sqrt{10}$，或z=6+$2\sqrt{10}$（舍去），
故2x-y∈[6-$2\sqrt{10}$，7]

点评 本题考查圆的方程，考查直线与圆的位置关系，线性规划，是解析几何与不等式的综合应用，难度中档．