
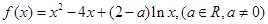
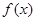 的单调区间;
的单调区间;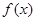 在区间
在区间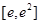 上的最小值.
上的最小值.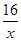 ,由f'(x)>0,解得x>4或一2<x<0,注意到x>0,所以函数f(x)的单调递增区间是(4,+∞).由f'(x)<0,解得0<x<4或x<-2.注意到x>0,所以函数f(x)的单调递减区间是(0,4).综上所述,函数f(x)的单调递增区间是(4,+∞),单调递减区间是(0.4).(2)当x∈[e,e2]时,f(x)=x2-4x+(2-x)lnx, f'(x)=2x-4+
,由f'(x)>0,解得x>4或一2<x<0,注意到x>0,所以函数f(x)的单调递增区间是(4,+∞).由f'(x)<0,解得0<x<4或x<-2.注意到x>0,所以函数f(x)的单调递减区间是(0,4).综上所述,函数f(x)的单调递增区间是(4,+∞),单调递减区间是(0.4).(2)当x∈[e,e2]时,f(x)=x2-4x+(2-x)lnx, f'(x)=2x-4+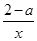 设g(x)=2x2-4x+2-a.当a<0时,有△=16-4×2(2-a)=8a<0,此时g(x)>0恒成立,所以f'(x)>0,f(x)在[e,e2]上单调递增,所以f(x)min=f(e)=e2-4e+2-a.当a>0时,△=16-4×2(2-a)=8a>0,令f'(x)>0,即2x2-4x+2-a>0,解得x>1+
设g(x)=2x2-4x+2-a.当a<0时,有△=16-4×2(2-a)=8a<0,此时g(x)>0恒成立,所以f'(x)>0,f(x)在[e,e2]上单调递增,所以f(x)min=f(e)=e2-4e+2-a.当a>0时,△=16-4×2(2-a)=8a>0,令f'(x)>0,即2x2-4x+2-a>0,解得x>1+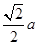 或x<1-
或x<1-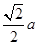 令f'(x)<0,即2x2-4x+2-a<0,解得1-
令f'(x)<0,即2x2-4x+2-a<0,解得1-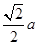 <x<
<x<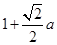 .①当
.①当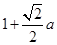 ≥e2,即a≥2(e2-1)2时,f(x)在区间[e,e2]上单调递减,所以f(x)min=f(e2)=e4-4e2+4-2a;②当e<
≥e2,即a≥2(e2-1)2时,f(x)在区间[e,e2]上单调递减,所以f(x)min=f(e2)=e4-4e2+4-2a;②当e<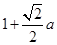 <e2,即2(e-1)2<a<2(e2-1)2时,在区间[e,
<e2,即2(e-1)2<a<2(e2-1)2时,在区间[e,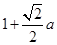 ]上单调递减,在区间[
]上单调递减,在区间[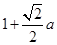 ,e2]上单调递增,所以f(x)min=f(
,e2]上单调递增,所以f(x)min=f(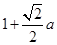 )=
)=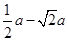 a-3+(2-a)ln(
a-3+(2-a)ln(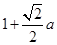 );③当
);③当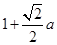 ≤e,即0<a≤2(e-1)2时,以f(x)在区间[e,e2]上单调递增,所以f(x)min=f(e)=e2-4e+2-a.综上所述,当a≥2(e2-1)2时,f(x)min=e4-4e2+4-2a;当2(e-1)2<a<2(e2-1)2时,f(x)min=
≤e,即0<a≤2(e-1)2时,以f(x)在区间[e,e2]上单调递增,所以f(x)min=f(e)=e2-4e+2-a.综上所述,当a≥2(e2-1)2时,f(x)min=e4-4e2+4-2a;当2(e-1)2<a<2(e2-1)2时,f(x)min=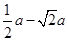 -3+(2-a)ln(
-3+(2-a)ln(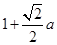 );当a<0或0<a≤2(e-1)2时,f(x)min=e2-4e+2-a.
);当a<0或0<a≤2(e-1)2时,f(x)min=e2-4e+2-a.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com