
【题目】已知函数![]() .
.
(Ⅰ)若f(1)=0,求函数f(x)的最大值;
(Ⅱ)令![]() ,讨论函数g(x)的单调区间;
,讨论函数g(x)的单调区间;
(Ⅲ)若a=2,正实数x1,x2满足![]() 证明
证明![]()
【答案】(1)f(x)的最大值为f(1)=0.(2)见解析(3)见解析
【解析】试题分析:(Ⅰ)代入求出![]() 值,利用导数求出函数的极值,进而判断最值;(Ⅱ)求出
值,利用导数求出函数的极值,进而判断最值;(Ⅱ)求出![]() ,求出导函数,分别对参数
,求出导函数,分别对参数![]() 分类讨论,确定导函数的正负,得出函数的单调性;(Ⅲ)整理方程
分类讨论,确定导函数的正负,得出函数的单调性;(Ⅲ)整理方程![]() ,观察题的特点,变形得
,观察题的特点,变形得![]() ,故只需求解右式的范围即可,利用构造函数,求导的方法求出右式的最小值.
,故只需求解右式的范围即可,利用构造函数,求导的方法求出右式的最小值.
试题解析:(Ⅰ)因为![]() ,所以a=-2,此时f(x)=lnx-x2+x,
,所以a=-2,此时f(x)=lnx-x2+x,
f'(x)=![]() -2x+1,
-2x+1,
由f'(x)=0,得x=1,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故当x=1时函数有极大值,也是最大值,所以f(x)的最大值为f(1)=0.
(Ⅱ)g(x)=f(x)-ax2-ax+1,
∴g(x)=lnx-![]() ax2-ax+x+1
ax2-ax+x+1 ![]() ,
,
当a=0时,g'(x)>0,g(x)单调递增;
当a>0时,x∈(0,![]() )时,g'(x)>0,g(x)单调递增;x∈(
)时,g'(x)>0,g(x)单调递增;x∈(![]() ,+∞)时,g'(x)<0,g(x)单调递减;
,+∞)时,g'(x)<0,g(x)单调递减;
当a<0时,g'(x)>0,g(x)单调递增;
(Ⅲ)当a=2时,f(x)=lnx+x2+x,x>0,.
由f(x1)+f(x2)+x1x2=0,即
lnx1+x12+x1+lnx2+x22+x2+x2x1=0.
从而(x1+x2)2+(x1+x2)=x1x2-ln(x1x2),.
令t=x2x1,则由φ(t)=t-lnt得,φ'(t)=![]() .
.
可知,φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.所以φ(t)≥1,
所以(x1+x2)2+(x1+x2)≥1,正实数x1,x2,
∴![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是长方形,侧棱
是长方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过D作
,过D作![]() 于F,过F作
于F,过F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)证明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中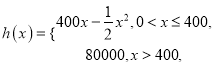
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)在某一个周期内的图象时,列表并填入的数据如下表:
x |
| x1 |
| x2 | x3 |
ωx+φ | 0 |
| π |
| 2π |
Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(1)求x1,x2,x3的值及函数f(x)的表达式;
(2)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,求函数y=f(x)·g(x)在区间![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
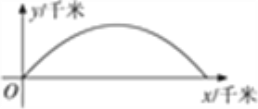
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.
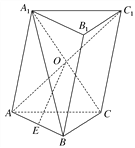
(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为![]() .
.
(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016年高考四川理数】设函数f(x)=ax2-a-lnx,其中a ∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com