
【题目】已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,且(a+b)(sinA﹣sinB)=(c﹣b)sinC (Ⅰ)求∠A的大小;
(Ⅱ)若f(x)= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ,求f(B)的取值范围.
,求f(B)的取值范围.
【答案】解:(I)∵(a+b)(sinA﹣sinB)=(c﹣b)sinC,由正弦定理可得:(a+b)(a﹣b)=(c﹣b)c,化为b2+c2﹣a2=bc. 由余弦定理可得:cosA= ![]() =
= ![]() =
= ![]() ,
,
∵A∈(0,π),∴A= ![]() .
.
(II)f(x)= ![]() =
= ![]() sinx+
sinx+ ![]() =
= ![]() +
+ ![]() ,
,
在锐角△ABC中, ![]() <B
<B ![]() ,∴
,∴ ![]() <B+
<B+ ![]() <
< ![]() ,
,
∴ ![]() ∈
∈ ![]() ,
,
∴f(B)的取值范围是 ![]()
【解析】(I)由(a+b)(sinA﹣sinB)=(c﹣b)sinC,由正弦定理可得:(a+b)(a﹣b)=(c﹣b)c,化为b2+c2﹣a2=bc.再利用余弦定理可得:cosA.(II)f(x)= ![]() sinx+
sinx+ ![]() =
= ![]() +
+ ![]() ,在锐角△ABC中,
,在锐角△ABC中, ![]() <B
<B ![]() ,可得
,可得 ![]() <B+
<B+ ![]() <
< ![]() ,即可得出.
,即可得出.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n2+2n,(n∈N*),求:
(1)数列{an}的通项公式an;
(2)若bn=an3n , 求数列{bn}的前n项和 Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么称
,那么称![]() 为闭函数.
为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是不是闭函数?若是请找出区间
是不是闭函数?若是请找出区间![]() ;若不是请说明理由;
;若不是请说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sinωx(>0)的图象向右平移 ![]() 个单位得到函数y=g(x)的图象,并且函数g(x)在区间[
个单位得到函数y=g(x)的图象,并且函数g(x)在区间[ ![]() ,
, ![]() ]上单调递增,在区间[
]上单调递增,在区间[ ![]() ]上单调递减,则实数ω的值为( )
]上单调递减,则实数ω的值为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+2x-6。
(1)证明:函数f(x)在其定义域上是增函数;
(2)证明:函数f(x)有且只有一个零点;
(3)求这个零点所在的一个区间,使这个区间的长度不超过![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数h(x),其中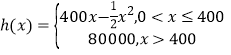 ,x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
,x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x),(a>1).
(1)求函数h(x)=f(x)﹣g(x)的定义域;
(2)求使f(x)﹣g(x)>0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,且点P(2,1)在椭圆C上. (Ⅰ)求椭圆C的方程;
,且点P(2,1)在椭圆C上. (Ⅰ)求椭圆C的方程;
(Ⅱ)若点A、B都在椭圆C上,且AB中点M在线段OP(不包括端点)上.求△AOB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com